Adversarial Cross-Modal Retrieval(ACMR)论文阅读笔记。

ACM MM 2017 Best Paper
本文提出了一个对抗跨模态检索方法(ACMR),基于对抗学习来寻找有效的共同子空间,模型的核心是两个过程间的相互作用,特征映射器和模态分类器。特征映射器主要进行表示学习的任务,也就是在公共子空间中,为不同模态的数据生成一个与模态无关的表示,它的目标是为了“迷惑”模态分类器。而模态分类器则是尝试分别数据的模态类型,从而引导特征映射器的学习。
此外,通过特征映射器的学习,可以保留跨模态数据潜在的语义结构,并且进行标签预测,这种方式可以保证学习到的特征表示在同一个模态中是有鉴别性的,又在跨模态中保持不变性。
对于跨模态间的结构不变性,之前提出的方法中,只关注了基于对的数据项的关系,而本文是通过利用模态之间更多的关系约束来解决的,即三元组约束。
ACMR方法
问题定义
- $n$ 个图像-文本对实例$\mathcal{O} = {o_i}_{i=1}^n$
- $o_i = (v_i, t_i)$
- 每个实例都有一个语义标签$y_i = [y_{i1},y_{i2},…,y_{ic}] \in \mathbb{R}^c$
- $\mathcal{O}$ 为所有实例图片、文本、标签矩阵的集合,其中$\mathcal{V} = {v_1,…,v_n}\in \mathbb{R}^{d_v \times n}$,$\mathcal{T} = {t_1,…,t_n} \in \mathbb{R}^{d_t \times n}$ 和 $\mathcal{Y} = {y_1,…,y_n} \in \mathbb{R}^{c\times n}$
由于图片特征和文本特征有着不同的统计属性和表示方式,两者服从的分布也很复杂,所以他们之间是不能直接进行比较的,为了能让他们能直接进行比较,我们的目标是找到一个共同的空间$\mathcal{S}$,将图片特征和文本特征映射到这个空间,$\mathcal{S_V} = f_{\mathcal{V}}(\mathcal{V};\theta_{\mathcal{V}})$ 和 $\mathcal{S_T} = f_{\mathcal{T}}(\mathcal{T};\theta_{\mathcal{T}})$,其中$f$ 为映射函数,$\mathcal{S_V},\mathcal{S_T} \in \mathbb{R}^{m\times n}$ 为图片和文本特征在$\mathcal{S}$ 中的表示。
方法提出
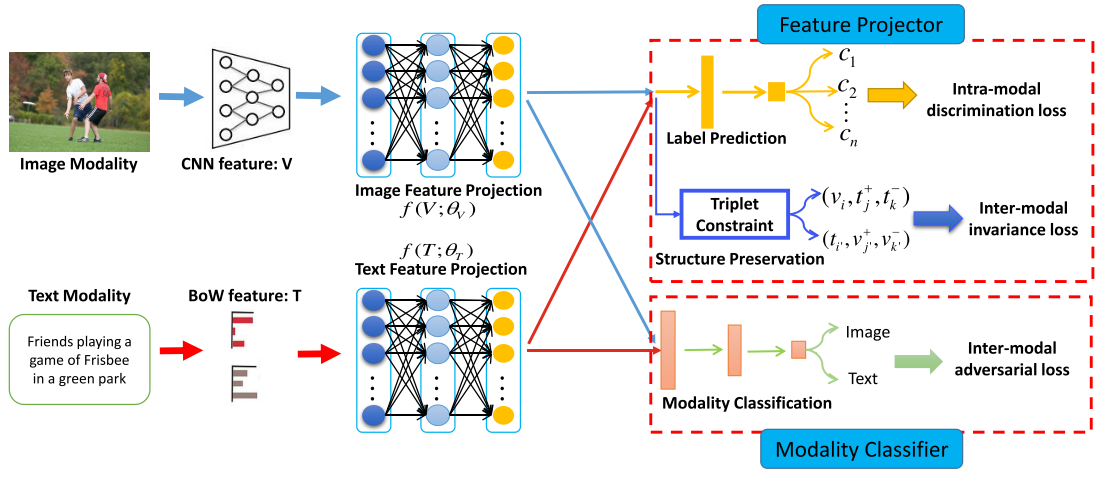
模态分类器(Modality Classifier)
作为GAN的判别器,将图片映射的特征标记为$\overline{01}$,文本映射的特征标记为$\overline{10}$,模态分类器 $D$ 的任务就是,给定一个特征映射,能够尽可能准确的判断它属于由哪一种模态映射而来。
分类的损失记作 adversarial loss ,即
\[\mathcal{L}_{adv}(\theta_D) = -\frac 1 n \sum_{i=1}^n(m_i \cdot (\log D(v_i;\theta_D) + \log(1-D(t_i;\theta_D)))\]- 交叉熵损失
- $m_i$ 是每个实例的真实模态标签
- $D(.;\theta)$ 实例 $o_i$ 中每一项(图像或文本)的模态判别概率
特征映射器(Feature Projector)
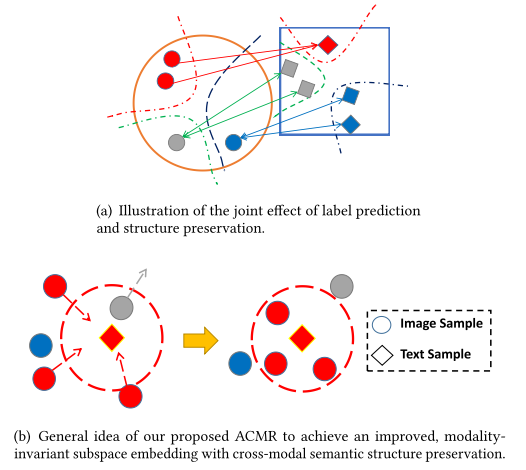
为了保证在共同子空间的图像和文本的modality-invariant,使用 label prediction 和 structure preservation 两个过程来对特征进行处理,Label prediction过程使得每个模态在共同子空间的映射特征通过语义标签区分开,即相当于模态内的分类;Structure preservation过程使得不同模态间有着同样的语义标签的特征保持不变。
如下图所示,(a) 中每个圆表示一个图像,每个方形表示一个文本,相同的颜色表示具有相同的语义分类,(b) 表示上述的两个过程。
Label Prediction
为了保证映射后模态内数据的区分度,使用一个分类器来预测映射后的特征所属的语义类别。在每个子空间映射网络之后,加上带有Softmax激活层的前馈神经网络作为分类器,这个分类器将映射后的图像文本对特征$o_i$作为输入,输出为每个类别的概率分布,用$\hat p$ 表示输出的概率分布,模态内的判别损失(intra-modal discrimination loss)为:
\[\mathcal{L}_{imd}(\theta_{imd}) = -\frac 1 n \sum_{i=1}^n (y_i \cdot (\log \hat p_i(v_i) + \log \hat p_i(t_i)))\]- $\mathcal{L}_{imd}$ 为交叉熵损失
- $n$ 为mini-batch的实例数目
- $y_i$ 是每个实例的真实语义标签
- $\hat p_i$ 是实例$o_i$ 中每一个项(图像或文本)的概率分布
Structure Preservation
为了保留模态间的相似不变性,我们的目标是使得不同模态间具有相同语义分类的数据特征的距离最小化,同时使得同一模态不同语义分类的数据的距离最大化。
通过三元组约束以及三元组损失函数来达到上述目标,映射后的特征的距离有$l_2$ 范数来度量:
\[l_2(v,t) = \|f_{\mathcal{V}}(v;\theta_{\mathcal{V}}) - f_{\mathcal{T}}(t;\theta_{\mathcal{T}})\|_2\]对每个语义标签$l_i$,采样三元组\(\{(v_i,t_j^+, t_k^-)\}_i\) 和 \(\{(t_i, v_j^+, v_k^-)\}_i\),$t_j^+$ 为与$v_i$的语义标签一致,而$t_k^-$ 的语义标签与$v_i$ 不同。
最后,计算模态间的不变性损失(inter-modal invariance loss):
\[\mathcal{L}_{imi,\mathcal{V}}(\theta_{\mathcal{V}}) = \sum_{i,j,k} l_2(v_i, t_j^+) + \lambda \cdot\max(0, \mu - l_2(v_i, t_k^-)) \\ \mathcal{L}_{imi,\mathcal{T}}(\theta_{\mathcal{T}}) = \sum_{i,j,k} l_2(t_i, v_j^+) + \lambda \cdot\max(0, \mu - l_2(t_i, v_k^-))\]将两者组合起来,得到
\[\mathcal{L}_{imi}(\theta_{\mathcal{V}},\theta_{\mathcal{T}}) = \mathcal{L}_{imi,\mathcal{V}}(\theta_{\mathcal{V}}) + \mathcal{L}_{imi,\mathcal{T}}(\theta_{\mathcal{T}})\]用于防止过拟合的正则化项如下
\[\mathcal{L}_{reg} = \sum_{l=1}^L (\|W_v^l\|_F + \|W_t^l\|_F)\]Feature Projector
特征映射的总体损失(将其记作embedding loss)为
\[\mathcal{L}_{emb}(\theta_{\mathcal{V}},\theta_{\mathcal{T}},\theta_{imd}) = \alpha\cdot \mathcal{L}_{imi} + \beta \cdot \mathcal{L}_{imd} + \mathcal{L}_{reg}\]对抗学习:优化
学习目标是使得adversarial loss 和 embedding loss 最小,将两者结合起来,使用 minimax game 来优化如下两个公式:
\[(\hat \theta_{\mathcal{V}}, \hat \theta_{\mathcal{T}}, \hat \theta_{imd}) = \mathop{\arg \max}_{\theta_{\mathcal{V}},\theta_{\mathcal{T}},\theta_{imd}} (\mathcal{L}_{emb}(\theta_{\mathcal{V}},\theta_{\mathcal{T}},\theta_{imd}) - \mathcal{L}_{adv}(\hat \theta_{D})), \\ \hat \theta_D = \mathop{\arg \max}_{\theta_D}(\mathcal{L}_{emb}(\hat\theta_{\mathcal{V}},\hat\theta_{\mathcal{T}},\hat\theta_{imd}) - \mathcal{L}_{adv}(\theta_{D}))\]- 使用SGD算法优化,如Adam
- Gradient Reversal Layer(GRL)
具体算法如下

实验
实现细节详见论文。

