Online asymmetric similarity learning for cross-modal retrieval

Cross-Modal Online Similarity function learning（CMOS）论文学习笔记。

CVPR 2017

本文提出了一个跨模态在线相关学习方法（CMOS），通过保留异构数据之间的语义相关性来学习他们的非对称的相关函数。数据间的语义相关性通过一系列在跨模态三元组数据上的双向铰链损失（hinge loss）约束来建模。

这个在线相关学习问题通过基于边距的在线PA（Passive-Aggressive）算法来解决，并且对大规模数据集展现了很好的扩展性。文中接着在再生核希尔伯特空间（reproducing kernel Hilbert space）中线性组合多个核函数来学习相关函数。

模型

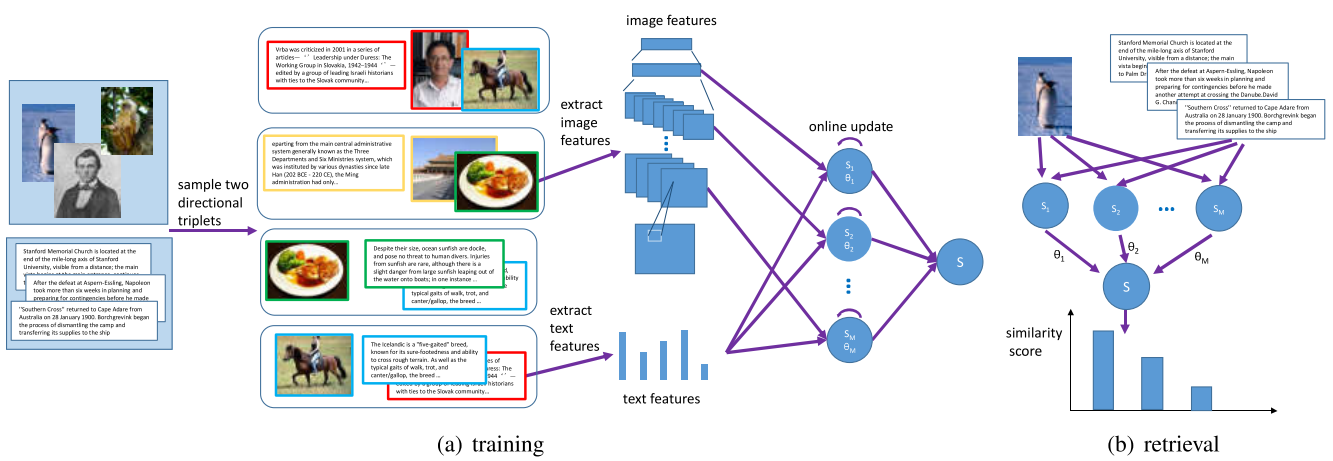
一些说明

• $\mathcal{V} = \{v_i\}_{i=1}^{N_v}$ 表示图片的集合
• $\mathcal{T} = \{t_i\}_{i=1}^{N_t}$ 表示文本的集合
• $v_i \in \mathbb{R}^{d_v}$，$t_i \in \mathbb{R}^{d_t}$ 都是列向量，这里的 $v_i, t_i$ 表示图像和文本的特征向量
• $r(v_i,t_j)$ 表示真实的语义相关对
• $(v_i, t_i^+, t_i^-) \in \prod^v$ 和 $(t_i, v_i^+, v_i^-) \in \prod^t$ 是表示相对相似关系的三元组
• $(v_i, t_i^+, t_i^-)$ 表示 $r(v_i, t_i^+) > r(v_i, t_i^-)$，称 $t_i^+$ 为正例，$t_i^-$ 为负例
• $\pi_i$ 表示一个任意类型的三元组

学习双向相对相似度

为什么要学习双向相似度

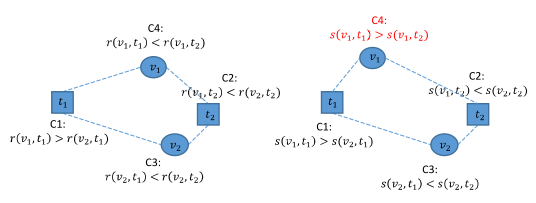
如上图所示，圆形和方形分别表示图像和文本，左边是四个数据的真实关系，右边是仅学习文本到图像方向的相关度得到的关系，由上图可以看出，学习可能只保证了C1和C2对C3和C4（从文本到图像方向）的相似度，而不能保证C3和C4从图像到文本方向的相似度。

因此，学习过程需要约束双向关系，即

$$s(v_i, t_i^+) > s(v_i, t_i^-), \quad \forall v_i \in \mathcal{V}, t_i^+,t_i^- \in \mathcal{T} \\ s(v_i^+, t_i) > s(v_i^-, t_i), \quad \forall t_i \in \mathcal{T}, v_i^+,v_i^- \in \mathcal{V}$$

其中，$s(v_i, t_j)$ 是一个非对称双线性函数，即

$$s(v_i, t_j) = v_i^T\mathbf{W}t_j$$

其中$\mathbf{W} \in \mathbb{R}^{d_v \times d_t}$ 不是方阵。

为了提高模型的泛华能力，对相对相似性引入margin，即

$$s(v_i, t_i^+) > s(v_i, t_i^-) + 1 \\ s(v_j^+, t_j) > s(v_j^-, t_j) + 1$$

对两个方向都定义 hinge loss，即

$$l_v(\mathbf{W};v_i, t_i^+, t_i^-) = \max\{0, s(v_i, t_i^-) - s(v_i, t_i^+) + 1\} \\ l_t(\mathbf{W};t_j, v_j^+, v_j^-) = \max\{0, s(v_j^-, t_j) - s(v_j^+, t_j) + 1\}$$

最终，我们的目标就是让训练数据的经验排序损失最小化，即

$$L(\mathbf{W};D_{train}) = \sum_{\pi_i\in \prod^v} l_v(\mathbf{W};v_i,t_i^+, t_i^-) + \sum_{\pi_i \in \prod^t} l_t(\mathbf{W};t_i, v_i^+, v_i^-)$$

Online学习算法

使用Passive-Aggressive（PA）算法来学习相似函数。PA算法是 margin-based 在线学习方法的总成，与随机梯度下降密切相关。

通过迭代的方法来学习$\mathbf{W}$，

• 首先，将$\mathbf{W}$初始化为全0矩阵
• 在每个迭代$i$，采样一个三元组$\pi_i \in \prod^v$ 或者 $\pi_i \in \prod^t$，然后按照以下方式更新

$$\mathbf{W}_i = \mathop{\arg \min}_\mathbf{W} \frac 12 \|\mathbf{W} - \mathbf{W}_{i-1}\|_F^2 + Cl_v(\mathbf{W}; v_i, t_i^+, t_i^-), \quad if \ \pi_i \in {\prod}^v$$ $$\mathbf{W}_i = \mathop{\arg \min}_\mathbf{W} \frac 12 \|\mathbf{W} - \mathbf{W}_{i-1}\|_F^2 + Cl_t(\mathbf{W}; t_i, v_i^+, v_i^-), \quad if \ \pi_i \in {\prod}^t$$

将上式看成一个约束问题，使用拉格朗日乘子来优化这个问题，两个式子的结果如下

$$\mathbf{W}_i = \mathbf{W}_{i-1} + \tau_i \mathbf{V}_i, \\ {\rm where}\ \mathbf{V}_i = v_i \times (t_i^+ - t_i^-)^T, \\ {\rm and}\ \tau_i = \min\{C, \frac{l_v(\mathbf{W}_{i-1};v_i, t_i^+, t_i^-)}{\|\mathbf{V}_i\|^2}\}$$

和

$$\mathbf{W}_i = \mathbf{W}_{i-1} + \tau_i \mathbf{V}_i, \\ {\rm where}\ \mathbf{V}_i = (v_i^+ - v_i^-) \times t_i^T, \\ {\rm and}\ \tau_i = \min\{C, \frac{l_t(\mathbf{W}_{i-1};t_i, v_i^+, v_i^-)}{\|\mathbf{V}_i\|^2}\}$$

具体算法如下（Eq.(6)和Eq.(7)即上面两式）

Online多核学习

由$\mathbf{W}$的更新式可知，当选择的三元组满足约束条件时，$\mathbf{W}$不更新，当选择的三元组不满足约束时，$\mathbf{W}$才更新。因此，

$$\mathbf{W} = \sum_{\pi_i \in {\prod}^v} \tau_i v_i (t_i^+ - t_i^-)^T + \sum_{\pi_i \in {\prod}^t}\tau_i(v_t^+ - v_i^-)t_i^T$$

给定两个新的数据$v$和$t$，二者的相似性可由下式计算

$$s(v,t) = \sum_{\pi_i \in {\prod}^v} \tau_i v^T v_i (t_i^+ - t_i^-)^T t + \sum_{\pi_i \in {\prod}^t}\tau_i v^T(v_t^+ - v_i^-)t_i^Tt$$

将内积替换成核函数，相似性函数可以重写为

$$\begin{align} s(v,t) = & \sum_{\pi_i \in {\prod}^v} \tau_i k^v(v, v_i)(k^t(t_i^+,t) - k^t(t_i^-,t)) + \\ & \sum_{\pi_i \in {\prod}^t}\tau_i(k^v(v, v_i^+) - k^v(v, v_i^-))k^t(t_i, t) \end{align}$$

• $k^v(\cdot, \cdot)$ 表示图像数据的核函数
• $k^t(\cdot, \cdot)$ 表示文本数据的核函数
• 可以使用高斯核函数或者多项式核函数等

在学习$\mathbf{W}$的时候不在记录$\mathbf{W}$，而是记录因子$\tau_i$和采样的三元组。在更新$\mathbf{W}$的方程中，使用核函数计算损失和$|\mathbf{V}_i|^2$，损失函数可直接由公式计算，$|\mathbf{V}_i|$计算如下：

$$\|\mathbf{V}_i\|^2 = k^v(v_i, v_i)[k^t(t_i^+, t_i^+) - 2k^t(t_i^-,t_i^+)+k^t(t_i^-, t_i^-)],\quad if\ \pi_i \in {\prod}^v \\ \|\mathbf{V}_i\|^2 = k^t(t_i, t_i)[k^v(v_i^+, v_i^+) - 2k^v(v_i^-,v_i^+)+k^v(v_i^-, v_i^-)],\quad if\ \pi_i \in {\prod}^t$$

接下来，我们使用多个核函数对应的相似函数的加权求和作为最终的相似函数。令$K = {(k_j^v, k_j^t), j = 1,…,M}$ 表示$M$对核函数的集合，我们需要的是学习这$M$个核函数对应相似函数线性组合的系数，同时也学习这个相似函数自身的参数$\tau$。

令$f(v,t) = \sum_{j=1}^M \theta_js_j(v,t)$为最终的相似函数，我们需要优化的目标就是使得所有相似函数的损失之和最小，即

$$\min_{\theta\in \Delta, \{s_j\}_{j=1}^M} \frac 12 \sum_{i=1}^M \|L_i\|_{HS}^2 + C(\sum_{\pi_i \in {\prod}^v} l_v(f; \pi_i) + \sum_{\pi_i \in {\prod}^t} l_t(f;\pi_i))$$

• $\Delta$ 是和为1的属于$(0,1)$的数的集合，即$\sum_{j=1}^M \theta_j = 1$
• $|\cdot|_{HS}$ 是线性因子的Hilbert Schmidt范数，正则化项

使用Hedging算法求解上述最优化问题的解，可以得到，在每次迭代时，对$M$对中的每一对核函数，使用下式来更新其参数

$$\theta_j(i) = \theta_j(i-1)\beta^{z_j(i)}$$

• $\beta \in (0, 1)$ 是折扣参数
• 当$s(v_i,t_i^+) - s(v_i,t_i^-) \le 0$ 或 $s(v_i^+, t_i) - s(v_i^-, t_i) \le 0$ 时 $z_j(i) = 1$，否则$z_j(i) = 0$

即当采样的三元组满足约束条件时，参数不更新，否则，参数按$\beta$衰减，即使得该相似函数的权重降低。

具体的算法如下（Eq.(6)和Eq.(7)同算法1）

实验

数据集

• Wiki dataset
  • 2,866 文本-图片对
  • 10个类别
  • 2,173 对作为训练集，693 对作为测试集
  • 文本使用10维 LDA 特征
  • 图片使用ImageNet训练的CNN抽取的特征 1,648维
• Pascal VOC 2007 dataset
  • 5000训练集，4919测试集，20个类别
  • 文本使用399维Bow特征
  • 3394维图片特征，由PCA之后的CNN抽取得到
• NUS-WIDE dataset
  • 10000训练集，5000测试集，10个类别
  • 文本使用1000维Bow特征
  • 3561维图片特征