DCMH论文阅读笔记。

CVPR 2018
模型结构
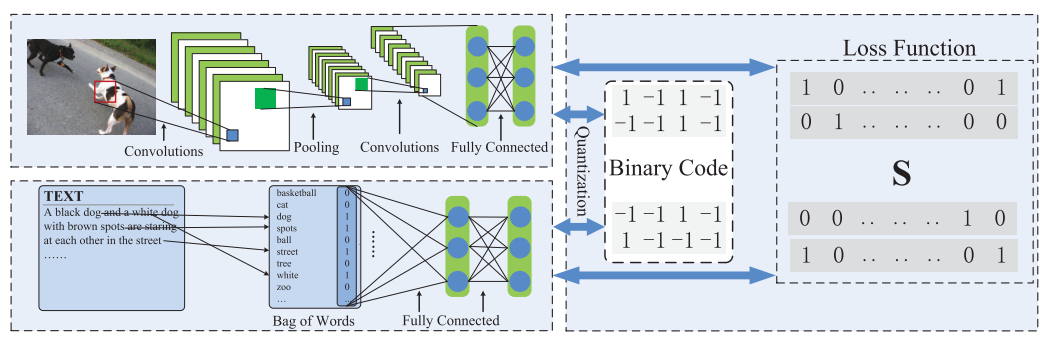
由两个部分组成:
- 特征学习部分
- Hash-code学习部分
- 在学习过程中,两个部分会相互反馈
特征学习部分
图像特征学习
使用的CNN由论文Return of the devil in the details: Delving deep into convolutional nets中继承而来,结构如下

- st. 表示步长
- LRN 表示是否使用Local Response Normalization
- 前7层都使用RELU作为激活函数,第8层没有激活函数
文本特征学习
使用词袋模型表示文本作为网络的输入,网络的结构如下:

- 第一层的激活函数是RELU,第二层直接输出
Hash-Code学习部分
令$f(\mathbf{x}_i;\theta_x) \in \mathbb{R}^c$和$g(\mathbf{y}_j;\theta_y)\in \mathbb{R}^c$分别表示图像特征网络和文本特征网络的输出,$\theta_x$和$\theta_y$分别是两个网络的参数。
DCMH的目标函数如下:
\[\begin{align} \min_{\mathbf{B}^{(x)}, \mathbf{B}^{(y)}, \theta_x, \theta_y} \mathcal{J} &= -\sum_{i,j=1}^n (S_{ij}\Theta_{ij} - \log(1+e^{\Theta_{ij}})) \\ & + \gamma(\|\mathbf{B}^{(x)} - \mathbf{F}\|_F^2 + \|\mathbf{B}^{(y)} - \mathbf{G}\|_F^2) \\ & + \eta(\|\mathbf{F1}\|_F^2 + \|\mathbf{G1}\|_F^2) \qquad \qquad \qquad \qquad (1)\\ s.t. \quad & \mathbf{B}^{(x)} \in \{-1,+1\}^{c\times n}, \\ & \mathbf{B}^{(y)} \in \{-1, +1\}^{c\times n} \end{align}\]- $\mathbf{F} \in \mathbb{R}^{c\times n}$,$\mathbf{F}_{*i} = f(\mathbf{x}_i; \theta_x)$
- $\mathbf{G} \in \mathbb{R}^{c\times n}$,$\mathbf{G}_{*j} = g(\mathbf{y}_j; \theta_y)$
- \[\Theta_{ij}=\frac{1}{2}\mathbf{F}_{*i}^T \mathbf{G}_{*j}\]
- $\mathbf{B}_{*i}^{(x)}$是图片$\mathbf{x}_i$的hash code
- $\mathbf{B}_{*j}^{(y)}$是文本$\mathbf{y}_j$的hash code
- $\gamma$和$\eta$是超参数
- $\mathbf{1}$ 是值全为1的列向量
(1) 式中第一项
\[-\sum_{i,j=1}^n (S_{ij}\Theta_{ij} - \log(1+e^{\Theta_{ij}}))\]负对数似然,其似然函数如下:
\[p(S_{ij}|\mathbf{F}_{*i},\mathbf{G}_{*j}) = \begin{cases} \sigma(\Theta_{ij}) & S_{ij} = 1 \\ 1 - \sigma(\Theta_{ij}) & S_{ij} = 0 \end{cases}\]其中,$\sigma(\Theta_{ij}) = \frac1{1+e^{-\Theta_{ij}}}$,经过变形,得
\[p(S_{ij}|\mathbf{F}_{*i},\mathbf{G}_{*j}) = \frac{e^{(S_{ij}-1) \Theta_{ij}}}{1+e^{-\Theta_{ij}}}\]- 最大化似然估计或者最小化负对数似然都可以达到目标,即当$S_{ij} = 1$时,\(\mathbf{F}_{*i}\) 和 \(\mathbf{G}_{*j}\) 的相似度(内积)越大,否则,他们的相似度越小
- 最终图片特征表示$\mathbf{F}$和文本特征表示$\mathbf{G}$可以保留相似性矩阵$\mathbf{S}$的内容
(1) 式中第二项
\[\gamma(\|\mathbf{B}^{(x)} - \mathbf{F}\|_F^2 + \|\mathbf{B}^{(y)} - \mathbf{G}\|_F^2)\]要使得该项最小,我们可以得到$\mathbf{B}^{(x)} = {\rm sign}(\mathbf{F})$,$\mathbf{B}^{(y)} = {\rm sign}(\mathbf{G})$。因为$\mathbf{F}$和$\mathbf{G}$都够保留$\mathbf{S}$中的相似性,所以$\mathbf{B}^{(x)}$和$\mathbf{B}^{(y)}$也能够达到相同的效果,而这正是跨模态哈希的目标。
(1) 式中第三项
\[\eta(\|\mathbf{F1}\|_F^2 + \|\mathbf{G1}\|_F^2)\]- 使得所有Hash code同一位的$+1$和$-1$的个数尽可能相等
- 因为$\mathbf{F,G} \in \mathbb{R}^{c \times n}$,$\mathbf{1} \in \mathbb{R}^{n \times 1}$,$\mathbf{F1}$ 的结果即是所有数据的Hash code对应的的每一位相加,得到长度为$c$的向量(或$c\times 1$的矩阵),然后平方求和,使之最小。
- 使得每一位bit提供的信息最大
改进
令$\mathbf{B}_{(x)} = \mathbf{B}_{(y)} = \mathbf{B}$,有:
\[\begin{align} \min_{\mathbf{B}, \theta_x, \theta_y} \mathcal{J} &= -\sum_{i,j=1}^n (S_{ij}\Theta_{ij} - \log(1+e^{\Theta_{ij}})) \\ & + \gamma(\|\mathbf{B} - \mathbf{F}\|_F^2 + \|\mathbf{B} - \mathbf{G}\|_F^2) \\ & + \eta(\|\mathbf{F1}\|_F^2 + \|\mathbf{G1}\|_F^2) \qquad \qquad \qquad \qquad (2)\\ s.t. \quad & \mathbf{B} \in \{-1,+1\}^{c\times n} \end{align}\]此为最终的目标函数。
- $\theta_x,\theta_y$和$\mathbf{B}$从同一个目标函数中学得
- 仅在训练阶段令$\mathbf{B}^{(x)} = \mathbf{B}^{(y)}$
学习策略
每次固定其他参数,只学习一个参数。
固定$\theta_y$和$\mathbf{B}$,学习$\theta_x$
使用BP算法学习参数$\theta_x$
首先计算梯度
\[\frac {\partial \mathcal{J}} {\partial \mathbf{F}_{*i}} = \frac 12 \sum_{j=1}^n (\sigma(\Theta_{ij})\mathbf{G}_{*j} - S_{ij}\mathbf{G}_{*j}) + 2\gamma(\mathbf{F}_{*i} - \mathbf{B}_{*i}) + 2 \eta \mathbf{F1}\]然后通过链式法则更新$\theta_x$。
固定$\theta_x$和$\mathbf{B}$,学习$\theta_y$
使用BP算法学习参数$\theta_y$
计算梯度
\[\frac {\partial \mathcal{J}} {\partial \mathbf{G}_{*j}} = \frac12 \sum(\sigma(\Theta_{ij})\mathbf{F}_{*i} - S_{ij}\mathbf{F}_{*i}) + 2\gamma(\mathbf{G}_{*j} - \mathbf{B}_{*j}) + 2 \eta \mathbf{G1}\]然后通过链式法则更新$\theta_y$。
固定$\theta_x$和$\theta_y$,学习$\mathbf{B}$
当$\theta_x$和$\theta_y$固定的时,(2) 式可转化为:
\[\begin{align} &\max_\mathbf{B} {\rm tr}\Big(\mathbf{B}^T\big(\gamma(\mathbf{F} + \mathbf{G})\big)\Big) = {\rm tr}(\mathbf{B}^T\mathbf{V}) = \sum_{i,j} B_{ij}V_{ij} \\ &s.t. \quad \mathbf{B}\in \{-1, +1\}^{c\times n} \end{align}\]其中$\mathbf{V} = \gamma(\mathbf{F}+\mathbf{G})$。
要使上式最大,$B_{ij}$应该与$V_{ij}$同号,因此:
\[\mathbf{B} = {\rm sign}(V) = {\rm sign}(\gamma(\mathbf{F} + \mathbf{G}))\]实验
数据集
- MIRFLICKR-25K dataset
- 25,000图片,每张图片有1到多个文本标签
- 选择至少有20个文本标签的图片用来实验
- 24个种类
- IAPR TC-12 dataset
- 20,000图片-文本对,255个种类
- 图片由句子描述
- NUS-WIDE dataset
- 选择195,834图像-文本对
- 含有至少同一种类标记的图片和文本视为相似的,否则不相似
评价方法
Hamming Ranking Protocols
将结果按照与查询的Hamming距离排序,计算最终的MAP值
Hash Lookup Protocols
返回与查询在一定Hamming redius范围内的所有结果,使用PR curve评价

