Latent Factor Hashing

本文就论文 Supervised Hashing with Latent Factor Models 和论文 Discrete Latent Factor Model for Cross-Modal Hashing 对 Latent Factor Hashing (LFH) 做简单总结。

泰勒公式

泰勒公式是将一个在 $x=x_0$ 出具有 $n$ 阶导数的函数 $f(x)$ 利用关于 $x-x_0$ 的 $n$ 次多项式来逼近函数的方法。

若函数 $f(x)$ 在包含 $x_0$ 的某个闭区间 $[a,b]$ 上具有 $n$ 阶导数，且在开区间 $(a,b)$ 上具有 $(n+1)$ 阶导数，则对闭区间 $[a,b]$ 上任意一点 $x$，成立下式：

\[f(x) = \frac{f(x_0)}{0!} + \frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2 + ... + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)\]

其中，$f^{(n)}(x)$ 表示 $f(x)$ 的 $n$ 阶导数，等号后的多项式称为函数 $f(x)$ 在 $x_0$ 处的泰勒展开式，剩余的 $R_n(x)$ 是泰勒公式的余项，是 $(x-x_0)^n$ 的高阶无穷小。

LFH

方法

论文 Supervised Hashing with Latent Factor Models 中提出了 LFH 方法，LFH 方法通过优化最大后验概率完成相似关系的提取。令 $\Theta$ 表示两个二进制码 $\mathbf{b}_i, \mathbf{b}_j$ 点积的一半，即：

\[\Theta_{i j}=\frac{1}{2} \mathbf{b}_{i}^{T} \mathbf{b}_{j}\]

因为汉明距离与向量內积之间存在以下的关系：

\[\operatorname{dist}_{H}\left(\mathbf{b}_{i}, \mathbf{b}_{j}\right)=\frac{1}{2}\left(Q-\mathbf{b}_{i}^{T} \mathbf{b}_{j}\right)=\frac{1}{2}\left(Q-2 \Theta_{i j}\right)\]

其中 $Q$ 为二值码长度。

则给定 $\mathbf{B}$ ，相似矩阵 $\mathcal{S}$ 的似然表示为：

\[p(\mathcal{S} | \mathbf{B})=\prod_{s_{i j} \in \mathcal{S}} p\left(s_{i j} | \mathbf{B}\right)\]

并且

\[p\left(s_{i j} | \mathbf{B}\right)=\left\{\begin{array}{ll}{a_{i j},} & {s_{i j}=1} \\ {1-a_{i j},} & {s_{i j}=0}\end{array}\right.\]

其中 $a_{ij} = \sigma(\Theta_{ij})$，$\sigma$ 是 logistic 函数，$\sigma = \frac{1}{1+e^{-x}}$。

一些方法直接通过优化最大似然来保留提取相似度，LFH则定义了 $\mathbf{B}$ 的先验概率 $p(\mathbf{B})$，则 $\mathbf{B}$ 的后验概率为：

\[p(\mathbf{B} | \mathcal{S}) \sim p(\mathcal{S} | \mathbf{B}) p(\mathbf{B})\]

使用最大后验概率进行相似度的保留，为了进行后续的优化，首先将二值矩阵 $\mathbf{B}$ 的约束放宽成实值矩阵 $\mathbf{U} \in \mathbb{R}^{N\times Q}$，$\Theta_{ij}$ 重定义为：

\[\Theta_{i j}=\frac{1}{2} \mathbf{U}_{i *} \mathbf{U}_{j *}^{T}\]

相似的，$p(\mathcal{S} \vert \mathbf{B}), p(\mathbf{B}), p(\mathbf{B} \vert \mathcal{S})$ 被替换为 $p(\mathcal{S} \vert \mathbf{U}), p(\mathbf{U}), p(\mathbf{U} \vert \mathcal{S})$。文中使用正态分布模拟 $\mathbf{U}$ 的先验分布，即：

\[p(\mathbf{U})=\prod_{d=1}^{Q} \mathcal{N}\left(\mathbf{U}_{* d} | \mathbf{0}, \beta \mathbf{I}\right)\]

则目标函数如下：

\[\begin{aligned} L &=\log p(\mathbf{U} | \mathcal{S}) \\ &=\sum_{s_{i j} \in \mathcal{S}}\left(s_{i j} \Theta_{i j}-\log \left(1+e^{\Theta_{i j}}\right)\right)-\frac{1}{2 \beta}\|\mathbf{U}\|_{F}^{2}+c \end{aligned}\]

优化

直接优化整个矩阵 $\mathbf{U}$ ，时间消耗太大，可以固定其他行，每次优化 $\mathbf{U}$ 的一行 $\mathbf{U}_{i*}$，我们可以找到 $L$ 的一个下界，然后最大化那个下界。这里就需要用到泰勒展开式，计算 $L$ 对 $\mathbf{U}_{i*}$ 的一阶梯度向量，以及Hessian矩阵如下：

\[\begin{aligned} \frac{\partial L}{\partial \mathbf{U}_{i *}^{T}}=& \frac{1}{2} \sum_{j : s_{i j} \in \mathcal{S}}\left(s_{i j}-a_{i j}\right) \mathbf{U}_{j *}^{T} \\ &+\frac{1}{2} \sum_{j : s_{j i} \in \mathcal{S}}\left(s_{j i}-a_{j i}\right) \mathbf{U}_{j *}^{T}-\frac{1}{\beta} \mathbf{U}_{i *}^{T} \\ \frac{\partial^{2} L}{\partial \mathbf{U}_{i *}^{T} \partial \mathbf{U}_{i *}}=&-\frac{1}{4} \sum_{j : s_{i j} \in \mathcal{S}} a_{j i}\left(1-a_{j i}\right) \mathbf{U}_{j *}^{T} \mathbf{U}_{j *} \\ &-\frac{1}{4} \sum_{j : s_{j i} \in \mathcal{S}} a_{j i}\left(1-a_{j i}\right) \mathbf{U}_{j *}^{T} \mathbf{U}_{j *}-\frac{1}{\beta} \mathbf{I} \end{aligned}\]

至于这里为什么要区分$s_{ij} \in \mathcal{S}$ 和 $s_{ji}\in \mathcal{S}$，是为了之后使用不同的学习策略时的统一表达，具体可以参见原论文。

定义

\[\mathbf{H}_{i}=-\frac{1}{16} \sum_{j : s_{i j} \in \mathcal{S}} \mathbf{U}_{j *}^{T} \mathbf{U}_{j *}-\frac{1}{16} \sum_{j : s_{j i} \in \mathcal{S}} \mathbf{U}_{j *}^{T} \mathbf{U}_{j *}-\frac{1}{\beta} \mathbf{I}\]

可以证明（三角不等式）：

\[\frac{\partial^{2} L}{\partial \mathbf{U}_{i *}^{T} \partial \mathbf{U}_{i *}} \succeq \mathbf{H}_{i}\]

其中 $\mathbf{A} \succeq \mathbf{B}$ 表示 $\mathbf{A} - \mathbf{B}$ 是半正定矩阵。

然后我们就可以使用 $L\left(\mathbf{U}_{i *}\right)$ 的二阶泰勒展开作为 $L\left(\mathbf{U}_{i *}\right)$ 的下界 $\widetilde{L}\left(\mathbf{U}_{i *}\right)$，即：

\[\begin{aligned} \widetilde{L}\left(\mathbf{U}_{i *}\right)=& L\left(\mathbf{U}_{i *}(t)\right)+\left(\mathbf{U}_{i *}-\mathbf{U}_{i *}(t)\right) \frac{\partial L}{\partial \mathbf{U}_{i *}^{T}}(t) \\ &+\frac{1}{2}\left(\mathbf{U}_{i *}-\mathbf{U}_{i *}(t)\right) \mathbf{H}_{i}(t)\left(\mathbf{U}_{i *}-\mathbf{U}_{i *}(t)\right)^{T} \end{aligned}\]

$\mathbf{U}_{i*}(t)$ 表示某个时间步 $t$ 的 $\mathbf{U}_{i*}$ 的值，为了使 $\widetilde{L}\left(\mathbf{U}_{i *}\right)$ 最大，只需要令 $\widetilde{L}\left(\mathbf{U}_{i *}\right)$ 对 $\mathbf{U}_{i*}^T$ 的梯度为0，即可得到：

\[\mathbf{U}_{i *}(t+1)=\mathbf{U}_{i *}(t)-\left[\frac{\partial L}{\partial \mathbf{U}_{i *}^{T}}(t)\right]^{T} \mathbf{H}_{i}(t)^{-1}\]

具体计算过程可参见附录，由此即可更新所有的行。

在本文中，作者提出了两种不同的优化策略（LFH-Full 和 LFH-Stochastic），两种方式分别使用全部的相似矩阵 $\mathcal{S}$ 和部分的相似矩阵（稀疏的相似矩阵 $\mathcal{S}$ 和对齐的相似矩阵 $\mathcal{S}$），如下图所示：

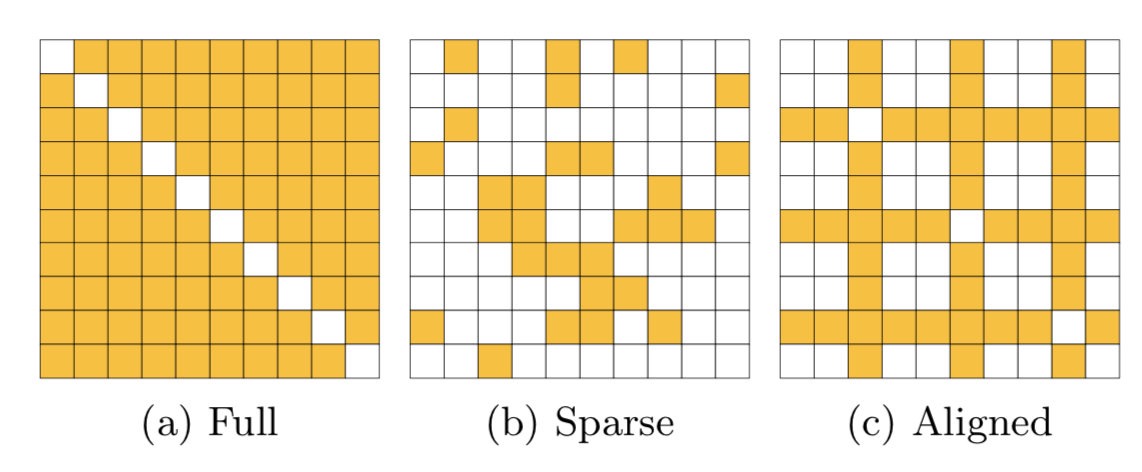
三种方式更新的复杂度依次降低，在使用第三种对齐的部分相似矩阵时，由于保证了 $\mathcal{S}$ 的对称性，$\mathbf{H}_i$ 可以简化为：

\[\mathbf{H}_{i}=-\frac{1}{8} \sum_{j : s_{i j} \in \mathcal{S}} \mathbf{U}_{j *}^{T} \mathbf{U}_{j *}-\frac{1}{\beta} \mathbf{I}\]

此时更新的复杂度为 $O(NQ^2)$，因为 $Q$ 的值相对较小，所以在大规模数据集上，LFH的扩展性很强。

当得到最优的 $\mathbf{U}$ 时，通过符号函数得到二值矩阵 $\mathbf{B}$。

Out-of-Sample

定义矩阵 $\mathbf{W}\in \mathbb{R}^{D\times Q}$，将查询 $\mathbf{x}$ 映射到实值向量 $\mathbf{u}$，即

\[\mathbf{u}=\mathbf{W}^{T} \mathbf{x}\]

然后使用符号函数得到二值向量 $\mathbf{b}$。

使用线性回归来学习矩阵 $\mathbf{W}$ 的值，$L_2$ 损失定义为：

\[L_{e}=\|\mathbf{U}-\mathbf{X} \mathbf{W}\|_{F}^{2}+\lambda_{e}\|\mathbf{W}\|_{F}^{2}\]

最优的 $\mathbf{W}$ 可由下式计算得到：

\[\mathbf{W}=\left(\mathbf{X}^{T} \mathbf{X}+\lambda_{e} \mathbf{I}\right)^{-1} \mathbf{X}^{T} \mathbf{U}\]

DLFH

论文 Discrete Latent Factor Model for Cross-Modal Hashing 提出了 DLFH 方法，与 LFH 相比主要有三点不同：

DLFH 进行的是跨模态哈希，而 LFH 则是单模态哈希
DLFH 是一种离散优化方法，直接学到二进制哈希码，而 LFH 则将二值放松到了实值
第三点是更新方式的不同，LFH 一次更新一个数据点的哈希码，而 DLFH 一次更新所有数据点的某一位哈希码，具体的更新方式在下文中介绍

方法

对于两个模态 $\mathbf{X}$ 和 $\mathbf{Y}$，以及他们之间的相似矩阵 $\mathbf{S} \in \{0, 1\}^{n\times n}$，我们的目标是学到两个模态的二值哈希码 $\mathbf{U}, \mathbf{V} \in \{-1,+1\}^{n\times c}$，其中 $c$ 是哈希码长度。定义 $\Theta_{ij} = \frac{\lambda}{c} \mathbf{U}_{i*}\mathbf{V}_{j*}$，其中 $\lambda$ 是超参。

需要注意的是，DLFH中的 $\mathbf{U}$ 和 LFH 中的 $\mathbf{U}$ 定义不同。

定义 $A_{ij} = \sigma(\Theta_{ij}) = \frac{1}{1+e^{-\Theta_{ij}}}$，基于 $A_{ij}$，我们定义相似度矩阵 $\mathbf{S}$ 的似然函数如下：

\[p(\mathbf{S} | \mathbf{U}, \mathbf{V})=\prod_{i, j=1}^{n} p\left(S_{i j} | \mathbf{U}, \mathbf{V}\right)\]

其中 $p\left(S_{i j} \vert \mathbf{U}, \mathbf{V}\right)$ 定义为：

\[p\left(S_{i j} | \mathbf{U}, \mathbf{V}\right)=\left\{\begin{array}{ll}{A_{i j},} & {\text { if } S_{i j}=1} \\ {1-A_{i j},} & {\text { otherwise }}\end{array}\right.\]

则对数似然为：

\[L=\log p(\mathbf{S} | \mathbf{U}, \mathbf{V})=\sum_{i, j=1}^{n}\left[S_{i j} \Theta_{i j}-\log \left(1+e^{\Theta_{i j}}\right)\right]\]

DLFH 的目标就是最大化对数似然，即优化下面的目标函数：

\[\begin{aligned} \max _{\mathbf{U}, \mathbf{V}} L &=\log p(\mathbf{S} | \mathbf{U}, \mathbf{V}) \\ &=\sum_{i, j=1}^{n}\left[S_{i j} \Theta_{i j}-\log \left(1+e^{\Theta_{i j}}\right)\right] \\ \text { s.t. }& \mathbf{U}, \mathbf{V} \in\{-1,+1\}^{n \times c} \end{aligned}\]

虽然其他一些方法也通过优化最大似然来提取跨模态相似度，但是这些方法都进行了放松处理，而 DLFH 则是直接进行的离散优化。

优化

因为有两个需要优化的矩阵，DLFH 采用交替优化的方式，每次固定一个矩阵，更新另一个矩阵。

固定 $\mathbf{V}$，优化 $\mathbf{U}$

DLFH 每次优化 $\mathbf{U}$ 的一列，即 $\mathbf{U}_{*k}$，为了达到这个目的，需要建立 $L(\mathbf{U}_{*k})$ 的一个下界，然后最大化这个下界。首先计算目标函数 $L$ 对于 $\mathbf{U}_{*k}$ 的梯度以及 Hessian 矩阵如下：

\[\left\{\begin{array}{l}{\frac{\partial L}{\partial \mathbf{U}_{* k}}=\frac{\lambda}{c} \sum_{j=1}^{n}\left(\mathbf{S}_{* j}-\mathbf{A}_{* j}\right) V_{j k}} \\ {\frac{\partial^{2} L}{\partial \mathbf{U}_{* k} \partial \mathbf{U}_{* k}^{T}}=-\frac{\lambda^{2}}{c^{2}} \operatorname{diag}\left(a_{1}, a_{2}, \cdots, a_{n}\right)}\end{array}\right.\]

其中 $\mathbf{A}=\left[A_{i j}\right]_{i, j=1}^{n}, a_{i}=\sum_{j=1}^{n} A_{i j}\left(1-A_{i j}\right)$，$\operatorname{diag}\left(a_{1}, a_{2}, \cdots, a_{n}\right)$ 表示对角矩阵。

令 $\mathbf{U}_{* k}(t)$ 表示第 $t$ 个迭代时 $\mathbf{U}_{* k}$ 的值，$\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)$ 表示 $\mathbf{U}_{* k}(t)$ 的梯度，$\mathbf{H} = -\frac{n\lambda^2}{4c^2}\mathbf{I}$，定义 $\widetilde{L}\left(\mathbf{U}_{* k}\right)$ 如下：

\[\begin{split} \widetilde{L}\left(\mathbf{U}_{* k}\right)&=&{L\left(\mathbf{U}_{* k}(t)\right)+\left[\mathbf{U}_{* k}-\mathbf{U}_{* k}(t)\right]^{T} \frac{\partial L}{\partial \mathbf{U}_{* k}}(t)} \\ & &+\frac{1}{2}\left[\mathbf{U}_{* k}-\mathbf{U}_{* k}(t)\right]^{T} \mathbf{H}\left[\mathbf{U}_{* k}-\mathbf{U}_{* k}(t)\right] \\ &=&\mathbf{U}_{* k}^{T}\left[\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)-\mathbf{H U}_{* k}(t)\right]-\left[\mathbf{U}_{* k}(t)\right]^{T} \frac{\partial L}{\partial \mathbf{U}_{* k}}(t) \\ & &+L\left(\mathbf{U}_{* k}(t)\right)+\frac{\left[\mathbf{U}_{* k}(t)\right]^{T} \mathbf{H} \mathbf{U}_{* k}(t)}{2}+\frac{\mathbf{U}_{* k}^{T} \mathbf{H U}_{* k}}{2} \\ &=&\mathbf{U}_{* k}^{T}\left[\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)-\mathbf{H} \mathbf{U}_{* k}(t)\right]-\left[\mathbf{U}_{* k}(t)\right]^{T} \frac{\partial L}{\partial \mathbf{U}_{* k}}(t) \\ & &+L\left(\mathbf{U}_{* k}(t)\right)+\frac{\left[\mathbf{U}_{* k}(t)\right]^{T} \mathbf{H} \mathbf{U}_{* k}(t)}{2}-\frac{\lambda^{2} n^{3}}{8 c^{2}} \\ &=&\mathbf{U}_{* k}^{T}\left[\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)-\mathbf{H U}_{* k}(t)\right]+\text { const } \end{split}\]

由于 $0<A_{i j}\left(1-A_{i j}\right)<\frac{1}{4}$，所以有 $\frac{\partial^{2} L}{\partial \mathbf{U}_{* k} \partial \mathbf{U}_{* k}^{T}}>\mathbf{H}$，故 $\widetilde{L}\left(\mathbf{U}_{* k}\right)$ 是 $L(\mathbf{U}_{*k})$ 的下界，然后，通过最大化 $\widetilde{L}\left(\mathbf{U}_{* k}\right)$ 来学习 $\mathbf{U}_{*k}$，即：

\[\begin{align} \max _{\mathbf{U} * k} \widetilde{L}\left(\mathbf{U}_{* k}\right)=&\mathbf{U}_{* k}^{T}\left[\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)-\mathbf{H U}_{* k}(t)\right]+\text { const } \\ \text { s.t. } &\mathbf{U}_{* k} \in\{-1,+1\}^{n} \end{align}\]

要使上式最大，只需要 $\mathbf{U}_{*k}$ 与 $\left[\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)-\mathbf{H U}_{* k}(t)\right]$ 每个元素同号即可，即 $\mathbf{U}_{* k}=\operatorname{sign}\left[\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)-\mathbf{H} \mathbf{U}_{* k}(t)\right]$，使用这个结果可以得到：

\[\mathbf{U}_{* k}(t+1)=\operatorname{sign}\left[\frac{\partial L}{\partial \mathbf{U}_{* k}}(t)-\mathbf{H U}_{* k}(t)\right]\]

固定 $\mathbf{U}$，优化 $\mathbf{V}$

同理可得：

\[\mathbf{V}_{* k}(t+1)=\operatorname{sign}\left[\frac{\partial L}{\partial \mathbf{V}_{* k}}(t)-\mathbf{H} \mathbf{V}_{* k}(t)\right]\]

其中，$\frac{\partial L}{\partial \mathbf{V}_{* k}}=\frac{\lambda}{c} \sum_{i=1}^{n}\left(\mathbf{S}_{i *}^{T}-\mathbf{A}_{i *}^{T}\right) U_{i k}$，$\mathbf{H}=-\frac{n \lambda^{2}}{4 c^{2}} \mathbf{I}$。

本文也提出了随机优化的策略（DLFH-Stochastic）用来降低更新复杂度，每个迭代通过随机选择相似矩阵的 $m$ 行（列）来计算 $\frac{\partial L}{\partial \mathbf{U}_{* k}}\left(\frac{\partial L}{\partial \mathbf{V}_{* k}}\right)$，则更新 $\mathbf{U}_{* k}$ 和 $\mathbf{V}_{* k}$ 如下：

\[\mathbf{U}_{* k}(t+1)=\operatorname{sign}\left[\frac{\lambda}{c} \sum_{q=1}^{m}\left(\mathbf{S}_{* j_{q}}-\mathbf{A}_{* j_{q}}\right) V_{j_{q} k}(t)+\frac{m \lambda^{2}}{4 c^{2}} \mathbf{U}_{* k}(t)\right] \\ \mathbf{V}_{* k}(t+1)=\operatorname{sign}\left[\frac{\lambda}{c} \sum_{q=1}^{m}\left(\mathbf{S}_{i_{q} *}^{T}-\mathbf{A}_{i_{q} *}^{T}\right) U_{i_{q} k}(t)+\frac{m \lambda^{2}}{4 c^{2}} \mathbf{V}_{* k}(t)\right]\]

其中，$\left\{j_{q}\right\}_{q=1}^{m}$ 和 $\left\{i_{q}\right\}_{q=1}^{m}$ 分别是采样的 $m$ 列和行。更新的复杂度会降低为 $O(mn)$，其中 $m \ll n$。

Out-of-Sample

文中使用线性和非线性两种分类器进行样本外扩展，对于线性分类器，最小化下面的平方损失：

\[L_{\text { square }}\left(\mathbf{W}^{(x)}\right)=\left\|\mathbf{U}-\mathbf{X} \mathbf{W}^{(x)}\right\|_{F}^{2}+\gamma_{x}\left\|\mathbf{W}^{(x)}\right\|_{F}^{2}\]

其中 $\gamma_x$ 正则项的超参，可以得到：$\mathbf{W}^{(x)}=\left(\mathbf{X}^{T} \mathbf{X}+\gamma_{x} \mathbf{I}\right)^{-1} \mathbf{X}^{T} \mathbf{U}$，哈希函数为：$h_{x}\left(\mathbf{x}_{q}\right)=\operatorname{sign}\left(\left[\mathbf{W}^{(x)}\right]^{T} \mathbf{x}_{q}\right)$。

对于非线性分类器，使用 kernel logistic regression (KLR) 进行分类，学习 $c$ 个分类器，每个分类器对应一个bit，用来预测 $\mathbf{x}_q$ 的二值码，对于第 $k$ 个bit，最小化下面的 KLR 损失：

\[L_{\mathrm{KLR}}\left(\mathbf{M}_{* k}^{(x)}\right)=\sum_{i=1}^{n} \log \left(1+e^{-U_{i k} \phi\left(\mathbf{x}_{i}\right)^{T} \mathbf{M}_{* k}^{(x)}}\right)+\eta_{x}\left\|\mathbf{M}_{* k}^{(x)}\right\|_{F}^{2}\]

其中 $\eta_x$ 是正则项的超参，$\phi(\mathbf{x}_i)$ 是 $\mathbf{x}_i$ 的 RBF 核特征表示，哈希函数为：$h_{x}\left(\mathbf{x}_{q}\right)=\operatorname{sign}\left(\left[\mathbf{M}^{(x)}\right]^{T} \phi\left(\mathbf{x}_{i}\right)\right)$。

参考文献

Zhang, Peichao, et al. “Supervised hashing with latent factor models.” Proceedings of the 37th international ACM SIGIR conference on Research & development in information retrieval. ACM, 2014.

Jiang, Qing-Yuan, and Wu-Jun Li. “Discrete Latent Factor Model for Cross-Modal Hashing.” IEEE Transactions on Image Processing (2019).

https://en.wikipedia.org/wiki/Matrix_calculus

https://en.wikipedia.org/wiki/Hessian_matrix

附录

梯度的计算。对式：

令 $\widetilde{L}\left(\mathbf{U}_{i *}\right)$ 对 $\mathbf{U}_{i*}^T$ 的梯度为0，即

\[\begin{align} \frac{d \widetilde{L}(\mathbf{U}_{i*})}{d\mathbf{U}_{i*}^T} &= \frac{\partial L}{\partial \mathbf{U}_{i*}^T}(t) + \frac12 [(\mathbf{H}_i(t) + \mathbf{H}_i(t)^T)\mathbf{U}_{i*}^T - \mathbf{H}_i(t)\mathbf{U}_{i*}(t)^T - \mathbf{H}_{i}(t)^T\mathbf{U}_{i*}(t)^T] \\ & = 0 \end{align}\]

因为 $\mathbf{H}_{i}(t)$ 是对称矩阵，所以上式可以写为：

\[\begin{align} \frac{d \widetilde{L}(\mathbf{U}_{i*})}{d\mathbf{U}_{i*}^T} &= \frac{\partial L}{\partial \mathbf{U}_{i*}^T}(t) + \mathbf{H}_i(t)^T\mathbf{U}_{i*}^T - \mathbf{H}_{i}(t)^T\mathbf{U}_{i*}(t)^T = 0 \end{align}\]

则有：

\[\mathbf{U}_{i*} = \mathbf{U}_{i*}(t) - [\frac{\partial L}{\partial \mathbf{U}_{i*}^T}(t)]^T\mathbf{H}_i(t)^{-1}\]