Production Quantization

Posted on | In | Visitors

Production Quantization（乘积量化）方法小结。

Production Quantization

目标

乘积量化的目标是对高维特征进行索引，减少特征存储消耗，同时加速检索速率。

Production Quantization

假设现在有特征向量 \(\mathbf{x} \in \mathbb{R}^d\)，首先将向量划分为 \(M\) 个子向量，\(\mathbf{x} = [\mathbf{x}_1, ..., \mathbf{x}_m, ..., \mathbf{x}_M],\ \mathbf{x}_m\in \mathbb{R}^{d/M}\)。

我们的目标是建立 \(M\) 个codebook，\(C = [C_1, ..., C_m, ..., C_M]\)，每个codebook由 \(k\) 个codeword 组成，即 \(C_m = [\mathbf{c}_{m1},...,\mathbf{c}_{mk}], \ \mathbf{c}_{mk} \in \mathbb{R}^{d/M}\)，注意，这里的每个codeword \(\mathbf{c}_{mk}\) 与子向量 \(\mathbf{x}_m\) 的维度相同，那么，codebook是怎么建立起来的呢？

Codebook

假设数据库中有 \(n\) 个数据，每个数据的特征维度为 \(d\)，这里介绍传统的无监督方法（k-means）来得到codebook。

如果需要生成 \(M\) 个codebook，每个codebook由 \(k\) 个codeword组成，则将 \(n\) 个数据中每个数据的特征划分成 \(M\) 份，即得到如下图所示的结果（图中 \(n=50K, d=1024, M=8\)）：

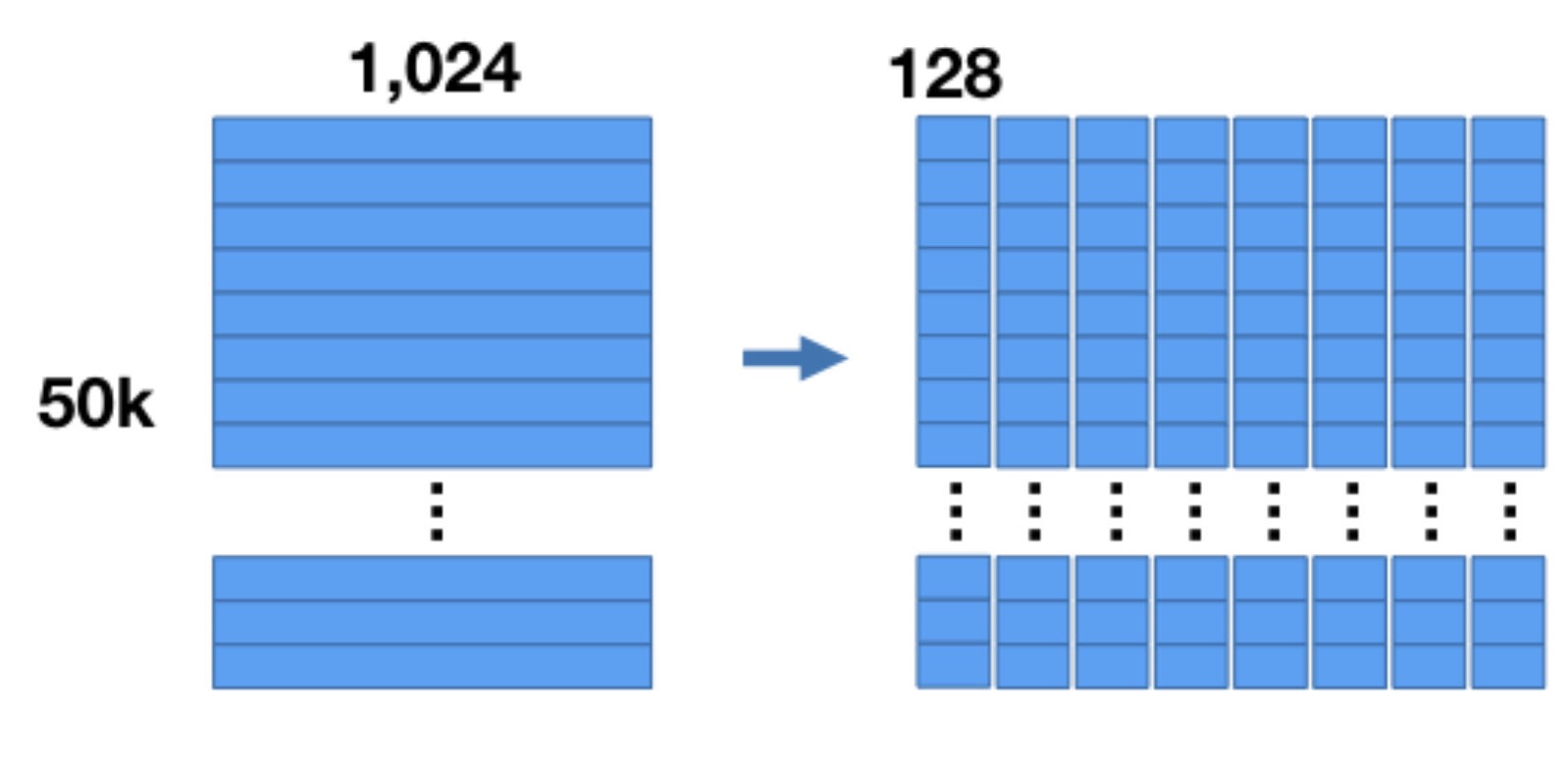
image-20181129160828141

此时得到 \(M\) 份 \(d/ M\) 维向量的集合，然后对每个集合进行k-means聚类，得到 \(k\) 类，即 \(k\) 的类别中心点，如下图所示（图中 \(k=256\)）：

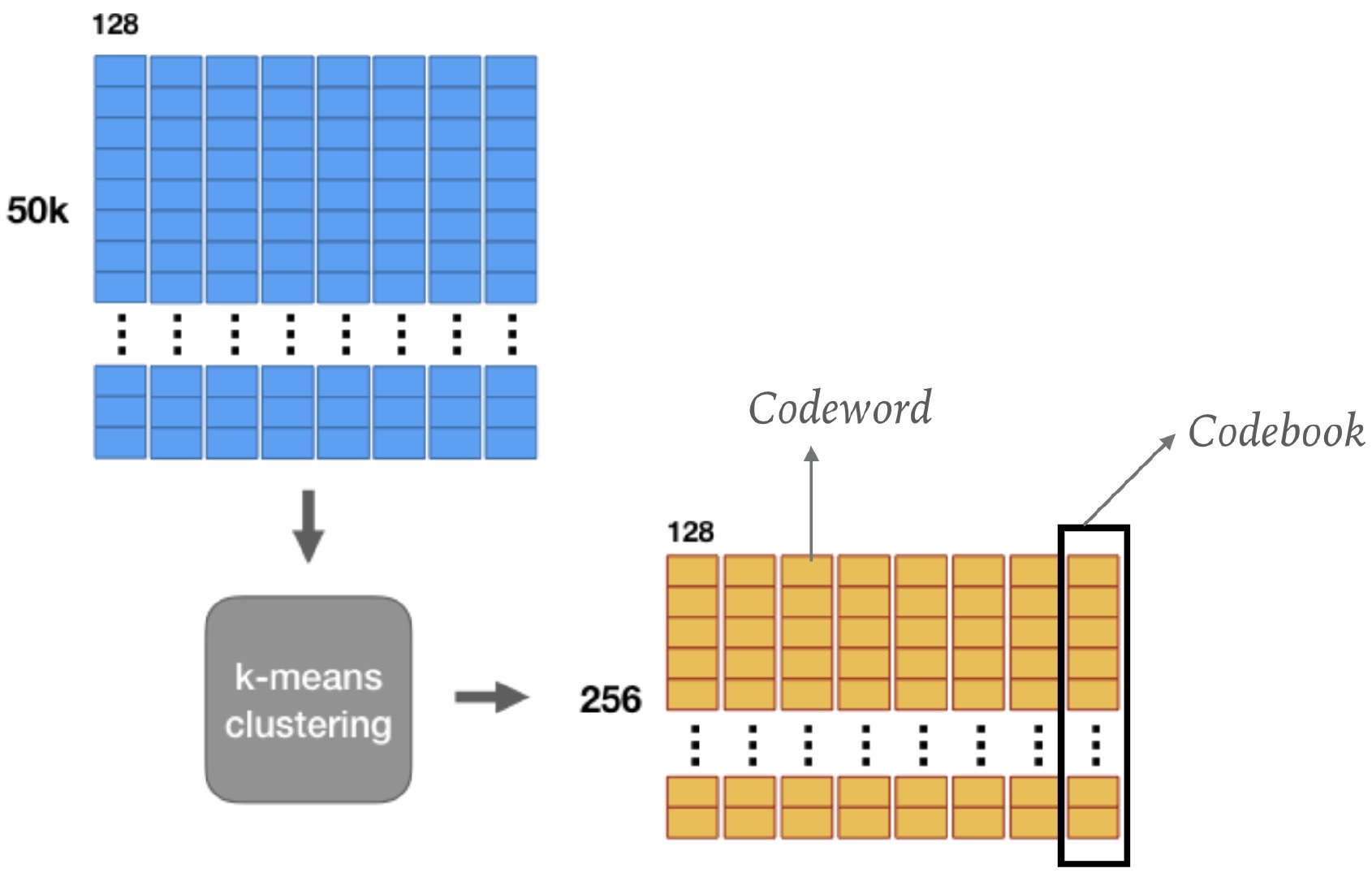
image-20181129161135067

即得到了codebook。

编码

建立了codebook之后，此时对于数据库的每个点 \(\mathbf{x} = [\mathbf{x}_1, ..., \mathbf{x}_m, ..., \mathbf{x}_M]\)，计算每个子向量 \(\mathbf{x}_m\) 与第 \(m\) 个codebook \(C_m\) 中每一个codeword \(\mathbf{c}_{mk}\) 的距离 \(d_{mk}\)，令

\[b_m = \mathop{\arg\min}_k d_{mk}\]

这里的距离 \(d_{mk} = \|\mathbf{x}_m - \mathbf{c}_{mk}\|_2^2\)，则最终 \(\mathbf{x}\) 就可以用得到的编码 \(\mathbf{b}\) 来表示，即

\[\mathbf{b} = [b_1,..., b_m, ..., b_M]\]

这样数据库中的每个点的子向量 \(\mathbf{x}_m\) 就可以用与其最近的中心点来代替，\(M\) 个子向量即组成了原向量 \(\mathbf{x}\)。

查询

那么对于一个查询点 \(\mathbf{q} = [\mathbf{q}_1, ..., \mathbf{q}_m, ...\mathbf{q}_M]\)，怎么返回与其近邻的数据点呢？首先计算每一个 \(\mathbf{q}_m\) 与 \(C_m\) 中每个codeword \(\mathbf{c}_{mk}\) 的距离，得到一张 \(k \times M\) 的距离表，然后对于数据库中的每个点 \(\mathbf{x}\)，\(\mathbf{q}\) 与 \(\mathbf{x}\) 的距离为：

\[d(\mathbf{q}, \mathbf{x}) = \sum_{m=1}^M \|\mathbf{q}_m, \mathbf{c}_{mb_m}\|_2\]

得到查询与数据库中所有点的距离之后进行排序，即可得到与其临近的数据点。

计算次数

  • 使用production quantization之前，需要 \(n\) 次 \(d\) 维的距离运算（方差运算）
  • 使用production quantization之后，需要进行 \(k \times M\) 次 \(d / M\) 维距离运算（方差运算）+ \(n \times M\) 次加法运算

Production Quantization Network

传统的方法是在得到数据点的特征之后，使用无监督方法得到乘积量化的codebook，但是这样得到的codebook无法保证保留准确的语义信息，因此有研究提出通过端到端的方式来同时学习特征表示和乘积量化。

模型的关键在于codebook是网络直接学到的，并且同时能够生成图片的特征表示，然后将学到的codebook运用到乘积量化方法中实现快速的图片检索。

image-20181129172146726

ECCV 2018

问题定义

  • \(\mathbf{x} \in \mathbb{R}^d\) 表示图片 \(I\) 的特征，将 \(\mathbf{x}\) 划分成 \(M\) 个子向量

    \[[\mathbf{x}_1, ..., \mathbf{x}_m, ..., \mathbf{x}_M]\]

  • \(\mathbf{x}\) 通过乘积量化近似表示为：

    \[\mathbf{q} = [q_1(\mathbf{x}_1, ..., q_m(\mathbf{x}_m), ..., q_M(\mathbf{x}_M)]\]

    其中，\(q_m(\mathbf{x}_m) = \sum_k \mathbb{I}(k=k^*)\mathbf{c}_{mk}\)

  • \(\mathbf{c}_{mk}\) 是第 \(m\) 个codebook中的第 \(k\) 个codeword，\(\mathbb{I}(\cdot)\) 是指示函数，满足条件时值为1

  • \[k^* = \arg \min_k \Vert\mathbf{c}_{mk}, \mathbf{x}_m\Vert_2\]

从硬量化到软量化

直接使用 \(\mathbb{I}(k=k^*)​\) 进行计算不能直接求导，所以不能直接整合到神经网络中。

将 \(\mathbb{I}(k=k^*)\) 替换为

\[\frac{e^{-\alpha \|\mathbf{x}_m - \mathbf{c}_{mk}\|_2^2}}{\sum_{k'} e^{-\alpha\|\mathbf{x}_m - \mathbf{c}_{mk'}\|_2^2}}\]

得到

\[\mathbf{x} = [s_1(\mathbf{x}_1), ..., s_m(\mathbf{x}_m),...,s_M(\mathbf{x}_M)]\]

其中

\[s_m(\mathbf{x}_m) = \sum_k \frac{e^{-\alpha \|\mathbf{x}_m - \mathbf{c}_{mk}\|_2^2}}{\sum_{k'} e^{-\alpha\|\mathbf{x}_m - \mathbf{c}_{mk'}\|_2^2}} \mathbf{c}_{mk}\]

不难证明

\[\mathbb{I}(k=k^*) = \lim_{\alpha \to +\infty}\frac{e^{-\alpha \|\mathbf{x}_m - \mathbf{c}_{mk}\|_2^2}}{\sum_{k'} e^{-\alpha\|\mathbf{x}_m - \mathbf{c}_{mk'}\|_2^2}}\]

模型

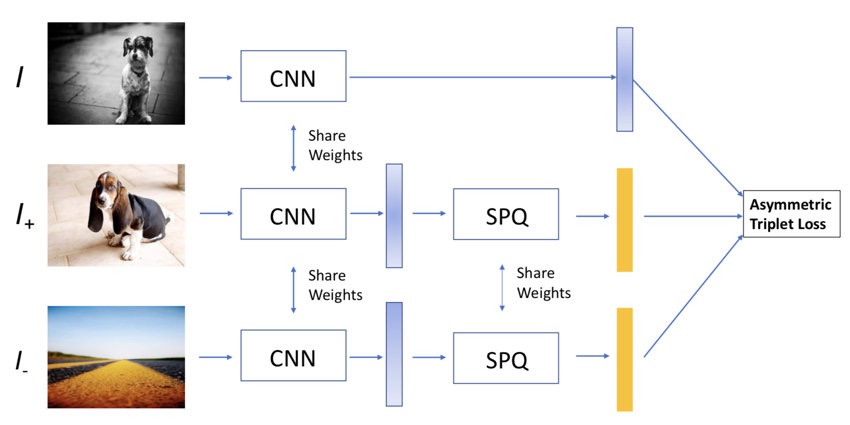
image-20181129174955089

SPQ: Soft Product Quantization layer

在进入SPQ层之前，先对特征 \(\mathbf{x} =[\mathbf{x}_1,...,\mathbf{x}_m, ...,\mathbf{x}_M]\) 和 codebook \(\{\mathbf{c}_{mk}\}_{m=1,k=1}^{M,K}\) 进行正则化，即

\[\mathbf{x}_m \leftarrow \mathbf{x}_m / \|\mathbf{x}_m\|_2 \\ \mathbf{c}_{mk} \leftarrow \mathbf{c}_{mk} / \|\mathbf{c}_{mk}\|_2\]

这样做的目的有两个：

  • 平衡每个子向量和每个codeword的贡献
  • 简化梯度的计算

在正则化之后，可以得到

\[\|\mathbf{x}_m - \mathbf{c}_{mk}\|_2^2 = 2 - 2\langle \mathbf{x}_m, \mathbf{c}_{mk}\rangle\]

和

\[s_m(\mathbf{x}_m) = \sum_k \frac{e^{2\alpha\langle \mathbf{x}_m, \mathbf{c}_{mk}\rangle}}{\sum_{k'}e^{2\alpha\langle \mathbf{x}_m, \mathbf{c}_{mk'}\rangle}}\mathbf{c}_{mk}\]

非对称三元组损失

  • 非对称

    • \(\mathbf{x}_I\) 是图片 \(I\) 没有经过SPQ的特征
    • \(\mathbf{s}_{I_+}\) 和 \(\mathbf{x}_{I\_}\) 是图片 \(I_+\) 和 \(I\_\) 经过SPQ的特征

  • 三元组损失

    \[l = \langle \mathbf{x}_I, \mathbf{s}_{I\_}\rangle - \langle \mathbf{x}_I, \mathbf{s}_{I_+} \rangle\]

    Sigmoid函数

    \[l = \frac{1}{1 + e^{\langle \mathbf{x}_I, \mathbf{s}_{I_+}\rangle - \langle \mathbf{x}_I, \mathbf{s}_{I\_} \rangle}}\]

编码和检索

给定数据库中的一张图片 \(I\)，得到图像Embedding层的输出\(\mathbf{x} = [\mathbf{x}_1,...,\mathbf{x}_m, ...,\mathbf{x}_M]\) 以及product quantization code \(\mathbf{b} = [b_1, ..., b_m, ..., b_M]\) ，其中

\(b_m = \mathop{\arg \max}_k\langle \mathbf{x}_m, \mathbf{c}_{mk}\rangle\) 在检索时，给定一个查询，通过图像Embedding层得到特征 \(\mathbf{q} = [\mathbf{q}_1,...,\mathbf{q}_m, ...,\mathbf{q}_M]\)，查询图片与数据库中图片的关系下式度量：

\[s(\mathbf{q}, \mathbf{b}) = \sum_{m=1}^M\langle \mathbf{q}_m, \mathbf{c}_{mb_m}\rangle\]

因为使用乘积量化方式降低了计算距离的复杂度，因此能够加快检索速率。

此时不赞何时赞！