Asymmetric Deep Supervised Hashing

Posted on | In | Visitors

Asymmetric Deep Supervised Hashing（ADSH）论文阅读笔记。

1536025638322

AAAI 2018

现有的很多深度哈希方法，都是采用对称策略来学习一个深度哈希函数，该函数同时对查询点和数据库点作用，在基于对的监督学习中，这种方法训练时的存储和计算成本都很大。为了使训练更高效，很多方法只是从整个大规模数据集中采样一小部分数据进行训练，使得检索效果不够好。

本文提出了一个深度有监督的哈希方法，即非对称深度监督哈希（ADSH）。

ADSH将查询点和数据库点做非对称地处理，只为查询点学习一个深度哈希函数，而数据库点的二进制表示直接学习得到。

问题定义

  • $\mathbf{X} = {x_i}_{i=1}^m$ 表示 $m$ 个查询数据点
  • $\mathbf{Y} = {y_j}_{j=1}^n$ 表示 $n$ 个数据库数据点
  • $\mathbf{S} \in {-1, +1}^{m\times n}$ 表示基于对的监督信息（相似度），当 $S_{ij}=1$ 时，表示点 $\mathbf{x}_i$ 和点 $\mathbf{y}_i$ 是相似的，否则不相似
  • $\mathbf{U} = {u_i}_{i=1}^m \in {-1, +1}^{m \times c}$ 表示为查询数据学到的二进制表示
  • $\mathbf{V} = {v_j}_{j=1}^n \in {-1,+1}^{n \times c}$ 表示为数据库点学到的二进制表示
  • $c$ 表示二进制码长度

为了使语义相似度得到保留，当 $S_{ij} = 1$ 时，$\mathbf{u}_i$ 和 $\mathbf{v}_j$ 的汉明距离必须尽可能小，否则，他们的汉明距离要尽可能大。此外，我们还应该学到一个哈希函数 $h(\mathbf{x}_q) \in {-1, +1}$，来为其他的查询数据（不在查询点集中）生成二进制码。

值得注意的是，在大多数情况下，只有一个大规模的数据库点集 $\mathbf{Y}$ 和点的相似度信息，我们可以通过在整个数据集上采样一个小的数据集或者直接使用整个数据集 $\mathbf{X}$ 作为查询点集，即 $\mathbf{X} \subseteq \mathbf{Y}$。

模型

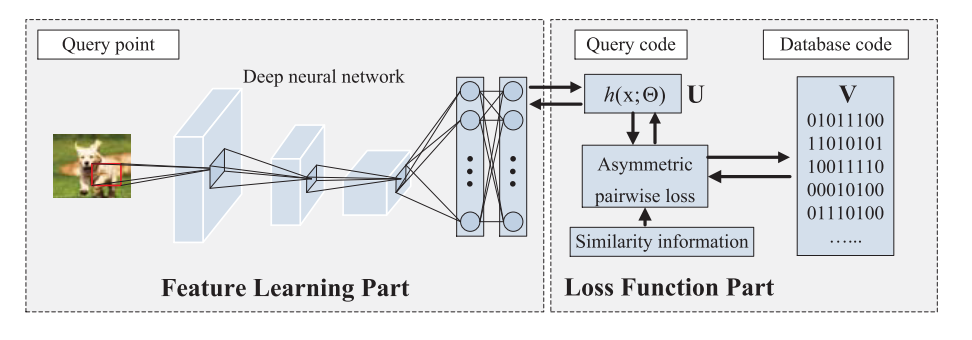
1536046054118

两个部分：

  • 特征学习部分
  • 损失函数部分

特征学习部分用来学习能够提取二进制码的近似特征表示的深度神经网络，损失函数部分则是为了学习能够保留查询点和数据库点之间语义相似度的二进制码。ADSH将两个部分整合到一个端到端的框架中，在训练过程中，两个部分相互进行反馈。

只有查询点集进行特征学习，这点和传统的深度哈希方法不一样，传统的深度哈希方法将查询点和数据库点在同一个神经网络上进行特征学习，然后再使用这个神经网络来为查询点和数据库点生成二进制码。

特征学习部分

使用经过ImageNet预训练的CNN-F模型作为特征提取器，将CNN-F的最后一层替换成一个将输出映射成 $\mathbb{R}^c$ 的全连接层。

当然，ADSH也可以使用其他的网络用来特征提取。

损失函数部分

为了学习能够保留数据相似度的哈希码，一个常用的方法就是最小化监督信息（相似度）与查询点二进制码和数据库点二进制码的内积的 $L_2$ 损失：

\[\min_{\mathbf{U}, \mathbf{V}} J(\mathbf{U}, \mathbf{V}) = \sum_{i=1}^m \sum_{j=1}^n (\mathbf{u}_i^T\mathbf{v}_j - cS_{ij})^2 \\ s.t.\quad \mathbf{U} \in \{-1, +1\}^{m\times c}, \mathbf{V} \in \{-1, +1\}^{n \times c}, \mathbf{u}_i = h(\mathbf{x}_i), \forall i\in\{1,2,...,m\}\]

然而，由于二进制码的离散性，直接学习 $h(\mathbf{x}_i)$ 很困难，令 $h(\mathbf{x}_i) = {\rm sign}(F(\mathbf{x}_i;\Theta))$ ，其中 $F(\mathbf{x}_i;\Theta) \in \mathbb{R}^c$。然后上式转化为：

\[\begin{align} \min_{\mathbf{\Theta}, \mathbf{V}}J(\Theta, \mathbf{V}) &= \sum_{i=1}^m \sum_{j=1}^n [h(\mathbf{x}_i)^T\mathbf{v}_j - cS_{ij}]^2 \\ & = \sum_{i=1}^m \sum_{j=1}^n [{\rm sign}(F(\mathbf{x}_i;\Theta))^Tv_j - cS_{ij}]^2 \\ s.t. \quad &\mathbf{v}_j = \{-1,+1\}^c, \forall j\in\{1,2,...,n\} \end{align}\]

将 $F(\mathbf{x}_i;\Theta)$ 作为 CNN-F 的输出，$\Theta$ 为CNN-F 的参数，这样可以将特征学习部分和损失函数部分无缝的整合在一起。

上式中还存在一个问题，不能对 ${\rm sign}(F(\mathbf{x}_i;\Theta))$ 求导，因此，使用 $\tanh(\cdot)$ 代替 ${\rm sign}(\cdot)$ ，有：

\[\begin{align} \min_{\mathbf{\Theta}, \mathbf{V}} J(&\Theta, \mathbf{V}) = \sum_{i=1}^m \sum_{j=1}^n [\tanh(F(\mathbf{x}_i;\Theta))^T\mathbf{v}_j - cS_{ij}]^2 \qquad (*)\\ s.t. \quad &\mathbf{V} \in \{-1, +1\}^{n \times c} \end{align}\]

实际中，可能只有一个数据集 $\mathbf{Y} = {y_j}_{j=1}^n$，没有查询点集，这种情况下，我们可以随机的从数据集中采 $m$ 个样本作为查询集 $\mathbf{X} = \mathbf{Y}^\Omega$ ，其中 $\Omega$ 表示点的索引。

我们使用 $\Gamma = {1, 2, …, n}$ 表示数据集所有点的索引， $\Omega = {i_1, i_2,…,i_m} \subseteq \Gamma$ 表示采取的查询点的索引，同样的，$\mathbf{S} = \mathcal{S}^\Omega$ ，$\mathcal{S} \in {-1,+1}^{n\times n}$ 表示数据集所有点的相似度，而 $\mathcal{S}^\Omega \in {-1,+1}^{m \times n}$ 则是 $\mathcal{S}$ 的子矩阵。

所以损失函数为：

\[\begin{align} \min_{\mathbf{\Theta}, \mathbf{V}} J(&\Theta, \mathbf{V}) = \sum_{i\in \Omega} \sum_{j\in\Gamma} [\tanh(F(\mathbf{y}_i;\Theta))^T\mathbf{v}_j - cS_{ij}]^2\\ s.t. \quad &\mathbf{V} \in \{-1, +1\}^{n \times c} \end{align}\]

由于 $\Omega \subseteq \Gamma$，对 $\forall i \in\Omega$，$\mathbf{y}_i$ 会产生两种表示，一个是整个数据集的二进制码 $\mathbf{v}_i$，一个是查询特征表示 $\tanh(F(\mathbf{y}_i;\Theta))$ 。所以我们加入了一个额外的约束，使得这两个表示尽可能的接近，由此得到最终的损失函数：

\[\begin{align} \min_{\mathbf{\Theta}, \mathbf{V}} J(\Theta, \mathbf{V}) = &\sum_{i\in \Omega} \sum_{j\in\Gamma} [\tanh(F(\mathbf{y}_i;\Theta))^T\mathbf{v}_j - cS_{ij}]^2 \\ & \gamma\sum_{i\in \Omega}[\mathbf{v}_i - \tanh(F(\mathbf{y}_i;\Theta))]^2 \qquad (\star) \\ s.t. \quad &\mathbf{V} \in \{-1, +1\}^{n \times c} \end{align}\]

其中 $\gamma$ 为超参。

在实际应用中，如果给定了 $\mathbf{Y}$ 和 $\mathbf{X}$ ，则使用 $(*)$ 式进行训练，如果只有 $\mathbf{Y}$，则使用 $(\star)$ 进行训练。

由于 $m \ll n$，所以ADSH训练非常高效，比传统的对称深度哈希方法要快。

学习策略

固定 $\mathbf{V}$ 学习 $\Theta$

使用BP算法学习 $\Theta$。

\[\frac{\partial J}{\partial \mathbf{z}_i} = \Big\{2\sum_{j\in\Gamma}\big[(\tilde{\mathbf{u}}_i^T \mathbf{v}_j - cS_{ij})\mathbf{v}_j\big] + 2\gamma(\tilde{\mathbf{u}}_i - \mathbf{v}_i)\Big\} \odot (1-\tilde{\mathbf{u}}_i^2) \qquad (6)\]

其中：

  • $\mathbf{z}_i = F(\mathbf{y}_i;\Theta)$
  • $\tilde{\mathbf{u}}_i = \tanh(\mathbf{z_i})$

然后就可以通过链式法则来计算 $\frac{\partial J}{\partial \Theta}$，然后更新 $\Theta$。

固定 $\Theta$ 学习 $\mathbf{V}$

当 $\Theta$ 固定时，将 $(\star)$ 式重为：

\[\begin{align} \min_\mathbf{V} J(\mathbf{V}) &= \|\tilde{\mathbf{U}}\mathbf{V}^T - c \mathbf{S}\|_F^2 + \gamma \|\mathbf{V}^\Omega - \tilde{\mathbf{U}}\|_F^2 \\ &= \|\tilde{\mathbf{U}}\mathbf{V}^T\|_F^2 - 2c{\rm tr}(\mathbf{V}^T\mathbf{S}^T\tilde{\mathbf{U}}) \\ &\qquad -2\gamma {\rm tr}(\mathbf{V}^\Omega \tilde{\mathbf{U}}^T) + {\rm const} \\ s.t. &\quad \mathbf{V} \in \{-1, +1\}^{n \times c} \end{align}\]

其中：

\[\tilde{\mathbf{U}} = [\tilde{\mathbf{u}}_{i_1},\tilde{\mathbf{u}}_{i_2},...,\tilde{\mathbf{u}}_{i_m}]^T \in [-1, +1]^{m \times c} \\ \mathbf{V}^\Omega = [\mathbf{v}_{i_1},\mathbf{v}_{i_2},...,\mathbf{v}_{i_m}]\]

定义：

\[\bar{\mathbf{U}} = \{\bar{\mathbf{u}}_j\}_{j=1}^n, \\ 其中，\bar{\mathbf{u}}_j = \begin{cases} \tilde{\mathbf{u}}_j & {\rm if} \ j\in\Omega \\ \mathbf{0} & {\rm otherwise} \end{cases}\]

然后将损失函数写为：

\[\begin{align} \min_\mathbf{V} J(\mathbf{V}) &= \|\mathbf{V}\tilde{\mathbf{U}}^T\|_F^2 - 2{\rm tr}\big(\mathbf{V}[c\tilde{\mathbf{U}}^T\mathbf{S} + \gamma\bar{\mathbf{U}}^T]\big) + {\rm const} \\ &= \|\mathbf{V}\tilde{\mathbf{U}}^T\|_F^2 + {\rm tr}(\mathbf{V}\mathbf{Q}^T) + {\rm const} \\ s.t. &\quad \mathbf{V} \in \{-1, +1\}^{n \times c} \end{align}\]

其中：

\[\mathbf{Q} = -2c\mathbf{S}^T\tilde{\mathbf{U}} -2 \gamma\bar{\mathbf{U}}\]

然后，按位（bit）更新 $\mathbf{V}$，就是说，每次只更新 $\mathbf{V}$ 的某一列，其他的列固定。令：

  • $\mathbf{V}_{*k}$ 表示 $\mathbf{V}$ 的第 $k$ 列
  • $\hat{\mathbf{V}}_k$ 表示除去第 $k$ 列的矩阵 $\mathbf{V}$，其他的符号含义类似

则我们需要解决的问题是：

\[\begin{align} \min_{\mathbf{V}_{*k}} J(\mathbf{V}_{*k}) &=\|\mathbf{V}\tilde{\mathbf{U}}^T\|_F^2 + {\rm tr}(\mathbf{V}\mathbf{Q}^T) + {\rm const} \\ &= {\rm tr}\big(\mathbf{V}_{*k}[2\tilde{\mathbf{U}}_{*k}^T\hat{\mathbf{U}}_k\hat{\mathbf{V}}_k + \mathbf{Q}_{*k}^T]\big) + {\rm const} \\ s.t. &\quad \mathbf{V}_{*k} \in \{-1, +1\}^n \end{align}\]

之后，我们得到上式的最优解：

\[\mathbf{V}_{*k} = -{\rm sign}(2\hat{\mathbf{V}}_k\hat{\mathbf{U}}_k^T\tilde{\mathbf{U}}_{*k} + \mathbf{Q}_{*k}) \qquad\qquad\qquad\qquad (10)\]

学习算法如下：

1536052603634

实验

细节见论文。

此时不赞何时赞！