Dual Deep Neural Networks Cross-Modal Hashing

Posted on | In | Visitors

Dual Deep Neural Networks Cross-Modal Hashing（DDCMH）论文阅读笔记。

1535355287172

AAAI 2018

DDCMH采用两个深度神经网络分别为不同的模态生成哈希码，不同于其他的深度哈希方法，DDCMH的两个神经网络分别单独进行优化，因此，它可以避免基于数据对进行训练所带来的问题。

DDCMH训练有三个阶段，第一个阶段，DDCMH利用单模态的Hash函数为训练集中文本模态的数据生成二进制码；第二阶段，有上一阶段生成的二进制码作为监督信息来训练将图像映射成二进制表示的神经网络；第三阶段，经过重构过程对图像模态数据的二进制码进行重构（为了获得高质量的Hash码），并将重构后的二进制码作为监督信息来训练另一个单模态文本网络，使之生成比第一阶段更好的文本模态数据的Hash码。

模型可以利用任意的单模态Hash方法，这意味着DDCMH可以作为框架，扩展单模态Hash方法来进行跨模态检索。

模型

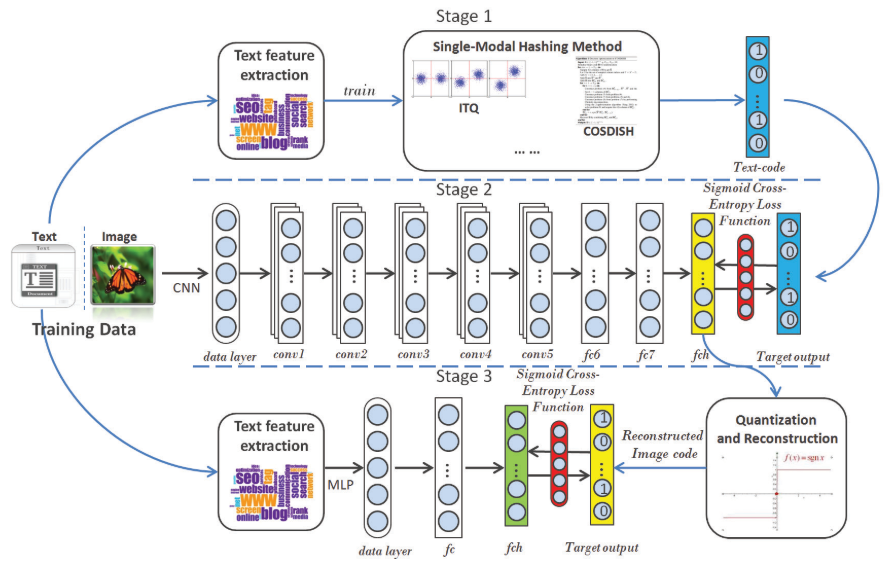
1535357033951

问题定义

  • 训练集

    • 图像：$\mathcal{X} = {x_i}_{i=1}^n$，$x_i \in \mathbb{R}^{D_x}$ 表示第$i$个图像数据的特征向量，为人工挑选的特征或者图像的原始像素
    • 文本：$\mathcal{Y} = {y_i}_{i=1}^n$，$y_i\in \mathbb{R}^{D_y}$ 表示第$i$个图像的文本标签信息
    • 图像的语义标签：$L = {l_i}_{i=1}^n$，$l_i\in \mathbb{R}^{D_l}$

  • 目标

    • 学习将图像 $x$ 和文本 $y$ 映射成 $k$ 位的Hash码的两个Hash函数 $f_x(\cdot)$ 和 $f_y(\cdot)$

    • $b_x = f_x(x)$，$b_y = f_y(y)$，$b_x,b_y \in {1,0}^k$

    • 符号函数

      \[sign(x) = \begin{cases} 1 & x > 0 \\ 0 & x \le 0 \end{cases}\]

DDCMH

阶段一：文本模态初始Hash码的生成

使用COSDISH方法作为文本的单模态Hash方法，训练之后，得到文本的Hash码：

\[B^{y1} = \{b_i^{y1}\}_{i=1}^n\]

阶段二：图像网络训练

将 $B^{y1}$ 作为监督信息，和原始图片一起训练一个深度神经网络，其实质上和多标签图像分类任务类似，即将 $B^{y1}$ 作为标签，学习从图像到Hash码 $B^x = {b_i^x}_{i=1}^n$ 的映射。

使用经过 ImageNet-1000 数据集预训练的 AlexNet 进行学习，原始的AlexNet包含 5 个卷积层（conv1-conv5）和 3 个全连接层（fc6-fc8），为获取图像的Hash码，将AlexNet的 fc8 层用一个新的有 $k$ 个结点的Hash层 fch，每个结点对应Hash码的一位。

令 $z_i^x = h_x(x_i;\theta_x)$ 为图像网络的输出，其中 $x_i$ 和 $\theta_x$ 分别是输入的图片和网络的参数。定义如下的似然函数：

\[p(b_{ij}^{y1}|z_{ij}^x) = \begin{cases} \sigma(z_{ij}^x) & b_{ij}^{y1} = 1 \\ 1-\sigma(z_{ij}^x) & b_{ij}^{y1} = 0 \end{cases}\]

  • $b_{ij}^{y1}$ 是 $B^{y1}$ 中第 $i$ 个数据的第 $j$ 位

  • $z_{ij}^x$ 第 $i$ 个数据在 fch 层第 $j$ 个结点的输出

  • $\sigma(\cdot)$ 是sigmoid函数

    \[\sigma(z_{ij}^x) = \frac{1}{1+e^{-z_{ij}^x}}\]

所以图像网络的损失函数如下：

\[\begin{align} L_x &= -\frac{1}{nk} \log p(B^{y1}|Z^x) \\ &= -\frac{1}{nk} \sum_{i=1}^n\sum_{j=1}^k \log p(b_{ij}^{y1}|z_{ij}^x) \\ &= -\frac{1}{nk} \sum_{i=1}^n \sum_{j=1}^k[b_{ij}^{y1}\log p_{ij}^x + (1-b_{ij}^{y1}) \log(1-p_{ij}^x)] \end{align}\]
  • $n$ 为训练样本数目
  • $k$ 为Hash码的位数
  • $p_{ij}^x = \sigma(z_{ij}^x)$

给定了上述的损失函数之后，我们使用BP算法，通过SGD优化参数 $\theta_x$。之后，我们得到训练集中图像的Hash码 $B^x = {b_i^x}_{i=1}^x$，其中 $b_i^x = sign(h_x(x_i;\theta_x))$。

阶段三：重构Hash码及文本网络训练

到此我们已经训练了两个模型，分别用来生成文本二进制码和图像二进制码，我们可以直接使用这两个网络对新的数据进行Hash，但是由于阶段一中生成的文本Hash码与图像模态的信息不相关，直接使用其进行跨模态检索可能得不到最优的结果，为解决这一问题，我们提出了阶段三的方法。

阶段三中，我们设计了一个有三层全连接层的感知机（MLP）作为文本网络。由于阶段二获得的图像的Hash码没有保留与文本显式的相关性，直接使用其对文本网络进行训练效果很差，但是因为提出的模型不使用基于数据对的信息，不能像其他深度Hash方法一样获取数据对之间的相关性。

为解决上述的问题，我们提出了Hash码重构的方法，按照语义标签来优化图像Hash码：

\[b_i^{xr} = \frac{1}{\|l_iL^T\|_1} l_iL^TB^x\]
  • $l_i$ 为第 $i$ 个图片的语义标签向量
  • $B^x$ 是阶段二生成的图像Hash码
  • $|\cdot|_1$ 为 $1$-范数
  • 重构的Hash码为 $B^{xr} = {b_i^{xr}}_{i=1}^n$

有着相同语义标签的数据会有相同的Hash码。

一旦给定了 $B^{xr}$，阶段三与阶段二的步骤类似，用 $B^{xr}$ 作为监督信息，文本特征作为输入来训练文本网络，最终得到文本模态数据 $\mathcal{Y}$ 的Hash码 $B^y = {b_i^y}_{i=1}^n$ 。

令 $z_i^y = h_y(y_i;\theta_y)$ 为文本网络的输出，$y_i$ 为输入，$\theta_y$ 为网络参数，网络的损失函数定义如下：

\[\begin{align} L_x &= -\frac{1}{nk} \log p(B^{xr}|Z^y) \\ &= -\frac{1}{nk} \sum_{i=1}^n\sum_{j=1}^k \log p(b_{ij}^{xr}|z_{ij}^y) \\ &= -\frac{1}{nk} \sum_{i=1}^n \sum_{j=1}^k[b_{ij}^{xr}\log p_{ij}^y + (1-b_{ij}^{xr}) \log(1-p_{ij}^y)] \end{align}\]

同样的，使用BP算法优化参数 $\theta_y$ 。

样本外扩展

对于不在训练集中的新的实例，给定图像查询 $x_q$，直接将其作为图像网络的输入，有

\[b_q^x = sign(h_x(x_q;\theta_x))\]

同样的，对于文本查询 $y_q$，使用文本网络，有

\[b_q^y = sign(h_y(y_q;\theta_y))\]

实验

详见论文。

此时不赞何时赞！