Deep Cross-media Knowledge Transfer(DCKT)论文阅读笔记

CVPR 2018
当前的跨模态检索方法通常需要依赖有标签的数据来训练模型,然而,收集跨模态数据并且标注是很耗费人力的事情,所以怎样将现有数据中有价值的信息迁移到新的数据中是应用中很重要的问题。
为实现这个目标,本文提出了深度跨媒体知识迁移(DCKT)方法,该方法能够将大规模跨模态数据集的信息迁移到小规模数据集中,用来提升在小规模跨模态数据集上模型的训练效果。
我们考虑下面的问题:在大规模跨模态数据集和另一个小规模数据集有着不同的标签空间时,应该怎样进行从大规模数据集(源域)到小规模数据集(目标域)的知识的迁移? DCKT方法的主要贡献如下:
双级别迁移架构,同时使得模态级别和相关度级别的域差异最小,将模态内语义和模态间相关知识进行迁移,来丰富训练信息,提高目标域的检索准确度;
渐进迁移机制,基于自适应反馈的跨媒体域一致性度量方法,根据目标域迁移难度的由易到难,迭代的选择训练样本。这种机制可以逐渐减少巨大的跨媒体域差异,增强模型的鲁棒性。
模型
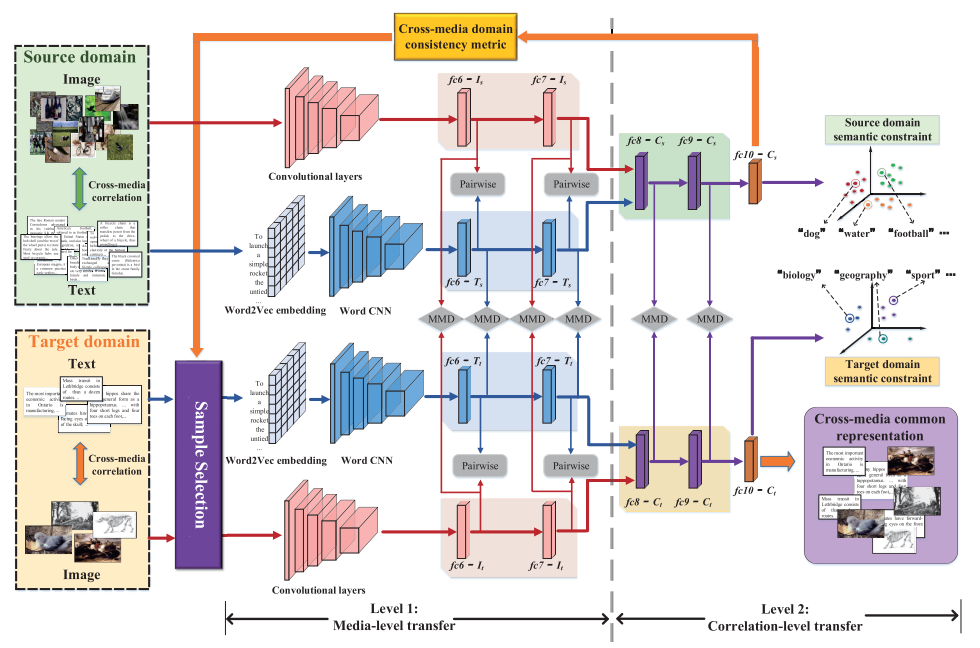
DKCT端到端的结构可以看成两个阶段:media-level迁移和correlation-level迁移。
- 源域:$Src = {(i_s^p, t_s^p),y_s^p}_{p=1}^P$,其中 $(i_s^p,t_s^p)$ 为标签为$y_s^p$的第$p$个图像-文本对。
- 目标域:\(Tar_{tr} = \{(i_t^q,t_t^q),y_t^q\}_{q=1}^Q\) 为训练集,\(Tar_{te} = \{(i_t^m, t_t^m)\}_{m=1}^M\) 为测试集
DCKT的目标就是同时利用 $Src$ 和 $Tar_{tr}$ 来训练模型,为 $Tar_{te}$ 的图像和文本生成共同的表示 $c_t(I)^m$ 和 $c_t(T)^m$,之后,跨媒体检索的距离计算就可以直接在共同的表示空间进行了。
Level 1: 模态级别的迁移
由于每个域都有两种类型的数据,所以域之间的差异主要来自两个方面:
- 模态级差异,即两个域中模态内的语义信息不同引起的差异;
- 相关性差异,即两个域中模态间的相关信息不同引起的差异。
模态级别的迁移,主要目标是针对模态级差异,通过 frature adaptation 实现两个域之间相同模态数据的迁移。
对每个域,图像和文本各有一条处理路径,并且连个域有同样的结构。在图像的处理部分,使用 VGG19 作为基本模型,保留 VGG19 除了最后的全连接层的所有层,源域中每个输入的图像转换为 4096 维的特征并通过 $fc6\text{-}I_s/fc7\text{-}I_s$ 层,目标域则通过 $fc6\text{-}I_t/fc7\text{-}I_t$ 层。
文本处理部分,首先将每个词通过 Word2Vec 转换为词向量,然后通过 Word CNN 从输入的文本向量生成 300 维的特征并经过 $fc6\text{-}T_s/fc7\text{-}T_s$ 和 $fc6\text{-}T_t/fc7\text{-}T_t$ 层。
通过最小化最大平均差异(minimize the maximum mean discrepancy,MMD)来实现两个域之间相同模态数据的 feature adaptation。
就图像来说,$I_s = {i_s}$ 和 $I_t = {i_t}$ 分别表示 $Src$ 和 $Tar_{tr}$ 的分布,$\mu_k(a)$ 表示在 reproducing kernel Hibert space(RKHS)$\mathcal{H}_k$ 空间中 $a$ 的均值,\(\mathbf{E}_{x\sim a} f(x) = \langle f(x), \mu_k(a)\rangle\),所以平方MMD \(m_k^2(I_s,I_t)\) 计算如下:
\[m_k^2(I_s,I_t) \triangleq \|\mathbf{E}_{I_s}[\phi(i_s, \theta_{I_s})] - \mathbf{E}_{I_t}[\phi(i_t, \theta_{I_t})]\|_{\mathcal{H}_k}^2\]- $\phi$ 表示网络的输出
- $\theta_x$ 表示网络参数
MMD 作用在两个域对应的层之间,即图像层$fc6\text{-}I_s/fc6\text{-}I_t$和 $fc7\text{-}I_s/ fc7\text{-}I_t$ ,文本层$fc6\text{-}T_s/fc6\text{-}T_t$ 和 $fc7\text{-}T_s/fc7\text{-}T_t$。最小化MMD,相同模态的域差异会被减少,并且知识迁移来说,两个域的单个模态的表示会被对齐。MMD 损失定义如下:
\[Loss_{MMD_I} = \sum_{l = l_6}^{l_7} m_k^2(I_s,I_t) \\ Loss_{MMD_T} = \sum_{l=l_6}^{l_7} m_k^2(T_s,T_t)\]每个域中的数据都是成对出现,即 $(i_s^p, t_s^p)$ 和 $(i_t^p, t_t^p)$ ,数据的共现表示语义的相似,所以通过减少他们表示的差异来保留这种约束,我们使用欧式距离作为距离度量,即
\[d^2(i_s^p,t_s^p) = \|\phi(i_s^p, \theta_{I_s}) - \phi(t_s^p, \theta_{T_s})\|^2 \\ d^2(i_t^q,t_t^q) = \|\phi(i_t^q, \theta_{I_t}) - \phi(t_t^q, \theta_{T_t})\|^2\]所以 pair-wise constraint loss 如下:
\[Loss_{Pair_s} = \sum_{l=l_6}^{l_7}\sum_{p=1}^P d^2(i_s^p, t_s^p) \\ Loss_{pair_t} = \sum_{l=l_6}^{l_7}\sum_{q=1}^Q d^2(i_t^q, t_t^q)\]通过使 MMD 损失和成对约束损失最小化,我们可以将源域中模态内的语义信息迁移到目标域中,同时还保留数据成对共线的相似关系。
Level 2: 相关性迁移
相关性迁移主要目标是将两个域中的模态间的相关性对齐。
在每个域中,图片和文本都将共用两个全连接层,共享的网络能够学习两个模态的语义信息,能够捕获模态间的关联性。我们在共享的网络间加入了 MMD 损失用来进行相关性迁移学习,MMD 损失计算如下:
\[Loss_{MMD_C} = \sum_{l=l_8}^{l_9} m_k^2(C_s, C_t)\]$C_s$ 和 $C_t$ 表示共享网络的输出。
同时,还需要保留语义信息以保持特征的语义辨识度,使用语义约束的 semantic loss :
\[Loss_{Se_s} = \sum_{p=1}^P(f_{sm}(i_s^p, y_s^p, \theta_{C_s}) + f_{sm}(t_s^p, y_s^p, \theta_{C_s})) \\ Loss_{Se_t} = \sum_{q=1}^Q(f_{sm}(i_t^q, y_t^q, \theta_{C_t}) + f_{sm}(t_t^q, t_t^q, \theta_{C_t}))\]- $\theta_{c_s}$ 是网络参数
- $f_{sm}$ 为softmax损失函数
渐进迁移机制(Progressive Transfer Mechanism)
上文介绍的所有的损失函数都可以使用SGD来优化,然而,由于两个域的标签空间差异很大,训练过程中可能产生很多的噪声和误导,尤其是在“空”模型上,所以我们提出渐进迁移机制逐渐降低跨模态域的差异。
为了从一个“安全”点开始,首先对每个域使用预训练的模型,并且移除所有链接两个域的 MMD 损失链接,为了方便,两个域的网络分别称为 $Model_s$ 和 $Model_t$ 。然后进行如下如所示的迭代过程,因为源域的数据规模相对较大,将 $Model_s$ 作为参考模型,在目标域中进行样本选择。在训练的早期阶段,我们从 $Tar_{tr}$ 中选择“简单”的样本(这些样本的跨模态关联性能够被 $Model_s$ 建模,与源域有着很高的一致性),举例来说,虽然标签空间不同,但是像“sport”和“football”这样的分类就有着很强的一致性。当模型稳定后,在后期的训练中再在目标模型中加入“更艰难”的样本。
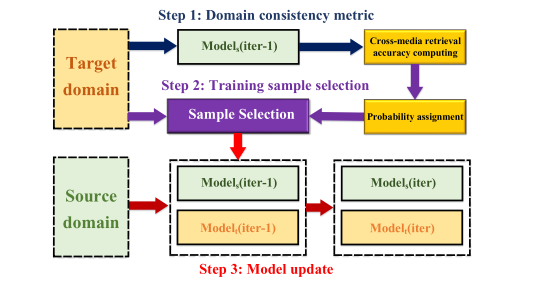
在每个迭代 $iter$ 中,通过 $Model_s(iter)$ 为 $Tar_{tr}$ 生成类别概率向量 $C_s$,包含 $C_s(I)$ 和 $C_s(T)$,然后使用图像-文本和文本-图像检索计算检索准确率,就图像-文本检索来说,计算每个图像 $c_s(I)^q$ 和 $C_s(T)$ 中每个文本的余弦距离,然后进行排序得到 $c_s(I)^q$ 的 AP 值:
\[AP(I)^q = \frac 1 R \sum_{k=1}^Q \frac{R_k}{k} \times rel_k\]- $R$ 是与 $c_s(I)^q$ 有着相同标签的文本的数目
- $R_k$ 是top-$k$ 相关文本的数目
- $rel_k$ 标识 $c_s(I)^q$ 和第 $k$ 个结果是否有相同的标签
$AP(I)^q$ 越高,表示 $Model_s(iter)$ 越成功的捕获了 $i_t^q$ 的跨模态关系,也就是源域中有着与 $i_t^q$ 紧密相关的知识,所以其可以看成是“简单”的样本。
同理,我们可以计算 $AP(T)^q$,然后得到
\[AP^q = AP(I)^q + AP(T)^q\]其中 $AP^q$ 可以用来估计 $(i_t^q, t_t^q)$ 的域一致性。训练过程中 $Model_s$ 迭代化的更新,所以 $AP^q$ 每轮迭代都需要重新计算,$AP^q$ 值高说明第 $q$ 个样本更适合作为两个域的桥梁,所以每个样本被选中的概率为:
\[Prob(q) = \alpha[1-\log_2(\frac{\max(AP) - AP^q}{\max(AP) \times iter} + 1)]\]- $\max(AP)$ 为$AP^q$ 的最大值
- $\alpha \in (0,1]$ 是 $Prob(q)$ 的上界,用来防止一直选择“最简单”的样本
当 $iter$ 增加的时候,$(\max(AP) - AP^q) / (\max(AP) \times iter)$ 的值将会变小,这意味着样本的选择将逐渐变为随机选择,具体算法如下:

训练结束后,每个测试数据都会被转化为共同空间的表示(实际是类别概率向量),然后使用距离函数来进行跨模态检索。在测试过程中,图片和文本单独的作为输入,并且标签和关联信息不再使用。
实验
细节见论文。

