UGACH论文阅读笔记

AAAI 2018
本文设计了一个基于图的无监督关联方法来捕获不同数据模态间潜在的相关结构,以及一个生成对抗网络来学习这个潜在的相关结构。
在UGACH方法中,给定任意模态数据,生成式模型会尝试拟合多模态之间潜在的相关关系的分布,然后从另一个模态选择相关数据来“骗过”判别器,而判别器模型则会学习去分辨输入是生成的相关数据还是真实的相关数据,真实的相关数据从相关图中采样得到。
文中提出了一个基于相关图的方法来获得不同模态的相关性,模态不同但是拥有相同语义的数据之间的Hamming距离会更小。我们将相关图融合到GAN中,为GAN提供数据的相关关系,来提高跨模态检索的准确度。
模型
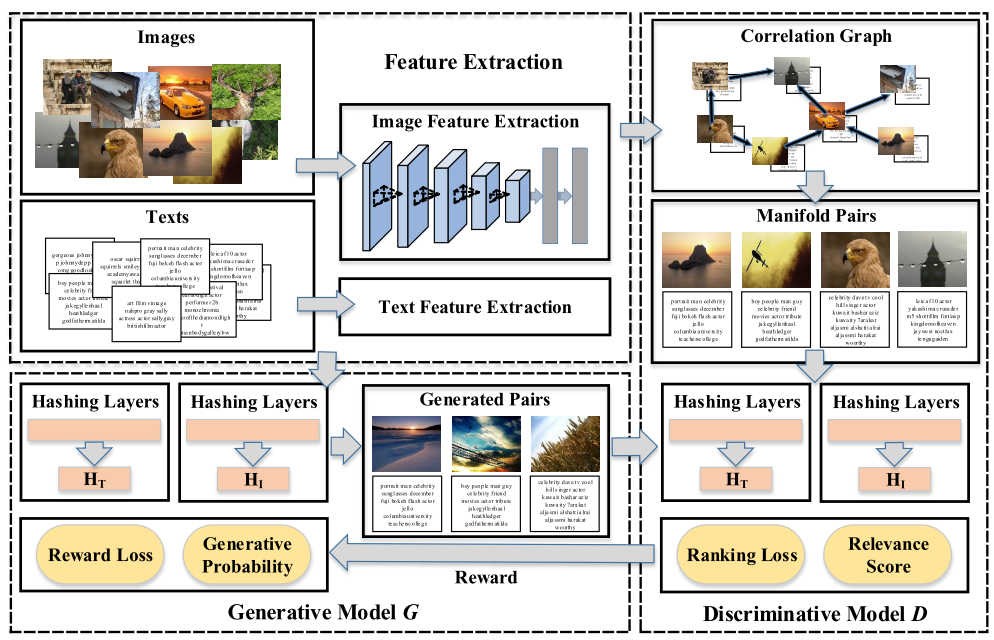
生成式模型
假设图像数据和文本数据的特征已经获得。
两层全连接层学习不同模态的表示:
-
Common Representation Layer
\[\phi_c(x) = \tanh(W_cx+b_c)\]$x$为图像或者文本。
-
Hashing Layer
\[h(x) = sigmoid(W_h\phi_c(x) + b_h)\]然后通过阈值函数获取二进制码
\[b(x) = sgn(h_k(x) - 0.5), \quad k = 1,2,...,l\]$l$为哈希码长度。由于直接对二进制码进行优化比较困难,所以在训练过程中对$h(x)$进行优化。
生成概率
生成模型的任务是给定一个模态的数据$q$,选择与真实相关分布一致的另一个模态的数据$x^U$,来通过判别模型的判别,其生成概率为
\[p_\theta(x^U|q) = \frac{\exp(-\|h(q) - h(x^U)\|^2)}{\sum_{x^U} \exp(-\|h(q)-h(x^U)\|^2)}\]判别式模型
相关图(Correlation Graph)
生成两个无向图$Grpah_i = (V, W_i)$和$Graph_t = (V, W_t)$分别表示文本和图像,其中$V$表示节点,$W$为相似矩阵,定义如下:
\[w(p,q) = \begin{cases} 1 & x_p \in NN_k(x_q) \\ 0 & otherwise \end{cases}\]$NN_k(x_q)$是$x_q$的$k$临近邻居的集合。
然后按照建立的相关图从真实数据分布中采样数据,对数据集中采样得到的某个数据对 $p_{true}(x|q^j)$ ,当 $w(k,j) = 1$ 时,选择 $x_k$ 作为查询 $q^j$ 的真实相关实例,并且将 $x_k$ 作为 manifold pair。
值得注意的是,跨模态数据中的成对信息存自然而然存在,因此如果文本查询 $q^j$ 与文本 $t_k$ 有着相同的潜在结构(即语义相似),则与 $t_k$ 成对的图像 $i_k$ 与 $q^j$ 也有着相同的潜在结构,反之亦然。
判别概率
收到生成的相关对和真实的相关对后,判别式模型给出每个对的得分作为判别结果。判别模型的输入是生成模型生成的图像-文本对和真实相关的图像-文本对,其任务是分别出两种图像-文本对,定义查询$q$和实例$x^G$的相关分数通过三元组排序损失定义如下:
\[f_\phi(x^G,q) = \max(0, m+\|h(q) - h(x^M)\|^2 - \|h(q) - h(x^G)\|^2)\]- $x^M$为相关图中真实相关的图像-文本对
- $x^G$为生成模型选择的实例
- $m$为margin值,实验中设置为1
- 上式的目标是使得真实相关对$(q,x^M)$的距离比生成对$(q,x^G)$的距离小$m$,以此可以清晰的判别两种图像-文本对
给定$q$,实例$x$的预测概率定义如下:
\[D(x|q) = sigmoid(f_\phi(x,q)) = \frac{\exp(f_\phi(x,q))}{1+\exp(f_\phi(x,q))}\]当$q$与$x$的相关得分越高时,$D(x|q)$越大,故判别式模型的目标是让$D(x^M|q)$更大,$D(x^G|q)$更小。
由于生成式模型是通过选择数据集中的数据来“挑战”判别式模型,这限制了其进行跨模态检索的能力,相反,判别式网络却很适合进行跨模态检索,故最终使用判别式模型生成的二进制码为检索所用。
对抗学习
\[\begin{align} \mathcal{V}(G,D) = & \min_\theta \max_\phi \sum_{j=1}^n (E_{x\sim p_{true}(x^M|q^j)}[\log(D(x^M|q^j))] \\ & + E_{x\sim p_\theta(x^G|q^j)}[\log(1-D(x^G|q^j))]) \end{align}\]判别式模型的目标是使上式最大化,而生成式模型的目标是使上式最小化。当判别式模型固定的时候,生成式模型可由以下方法学习:
\[\begin{align} \theta^* =\ & \mathop{\arg \min}_\theta \sum_{j=1}^n (E_{x\sim p_{true}(x^M|q^j)}[\log(sigmoid(f_{\phi^*}(x^M,q^j)))] \\ & +E_{x\sim p_\theta(x^G|q^j)}[\log(1-sigmoid(f_{\phi^*}(x^G,q^j)))]) \end{align}\]$f_{\phi^*}$表示上一轮迭代中的判别式模型相关得分函数,本模型从未打标签的数据中选择生成图片-文本对,由于选择策略是离散的,因此不同使用传统的SGD优化方法,故使用强化学习方法来学习生成模型的参数。
实验
数据集
- NUS-WIDE
- 共269,498图片-文本对,81个分类
- 选择10大类,186,557图片-文本对
- 全部数据的1%作为查询集合,剩下的为检索数据
- 每个图片表示为4096维向量,从19-leyer VGGNet提取
- 每个文本表示为1000维BoW向量
- MIRFlickr
- 25,000图片-文本对,24个分类
- 全部数据的5%作为查询集合,剩下的为检索数据

